Nemes Tihamér OKSzTV'2002

1. feladat: Villamos (20 pont) /tesztadatok/

Egy négyzetrács-szerkezetű városban különleges villamosok közlekednek, ugyanis olyan pályán járnak, amelynek a négyzet alakú elemeit el tudják forgatni. Az elemek a következők:

Minden elem négyféle helyzetben állhat:

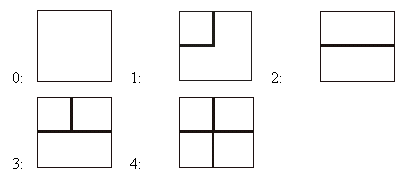
0: az ábrán látható módon
1: 90 fokkal jobbra elforgatva
2: 180 fokkal jobbra elforgatva
3: 270 fokkal jobbra elforgatva

Feladat:

Írj programot (VILLAMOS.PAS, VILLAMOS.C vagy VILLAMOS.CPP néven), amely megadja, hogy a villamos egy adott helyről egy másikra minimálisan hány lépésben (azaz a kezdőhelyet nem számítva hány elem érintésével) juthat el, illetve minimálisan hány lépésben juthat el akkor, ha azt az elemet, amelyen éppen áll, el tudja forgatni jobbra 90 fokkal! (Figyelem: a forgatás is lépésnek számít. Ugyanaz az elem több lépésben többször egymás után is elforgatható jobbra 90 fokkal.)

Bemenet:

A VILLAMOS.BE állomány első sorában a négyzetrács sorainak (1<=N<=100) és osz-lopainak (1<=M<=100) a száma van. A következő N sorban soronként M számjegy-pár (két szorosan egymás mellé írt számjegy) található egy-egy szóközzel elválasztva; mindegyik sor a négyzetrács egy sorát írja le. A négyzetrács minden elemét a fenti ábrán megadott azonosító számból és az elforgatás kódjából álló számjegy-párral adjuk meg.

A bemenő állomány utolsó sorában négy egész szám van: a kezdőhely sor- és oszlopindexe, valamint a célhely sor- és oszlopindexe.

Kimenet:

A VILLAMOS.KI állomány első sorába azt a minimális lépésszámot kell írni, amely elegendő ahhoz, hogy a villamos eljusson a kezdőhelyről a célhelyre; a második sorba pedig ugyanezt a számot abban az esetben, ha a villamos elforgathatja azt az elemet, amelyen éppen áll vagy áthalad. A lépésszám legyen –1, ha nem lehet eljutni a kezdőhelyről a célhelyre!

Példa:

Megjegyzés:

Út az 1. esetben: (1,2),(2,2),(2,3),(2,4),(2,5),(3,5),(4,5),(4,4),(4,3),(4,2),(4,1)
Út a 2. esetben: (1,2),(2,2),(2,1),fordít,(3,1),fordít,(4,1)

2. feladat: Mozgat (20 pont) /tesztadatok/

Minden szövegszerkesztővel végezhető kivágás-beszúrás művelet. Minden műveletet egy A, B, C számhármas ír le, ami azt jelenti, hogy a szöveg A-tól B-ig terjedő sorait (A-t és B-t is beleértve) kivágjuk, és beszúrjuk a C-edik sor mögé. (Az A, B és C sorszámok a művelet elvégzése előtt értendők.)

Feladat:

Egy N sorból álló szövegre K-szor alkalmazunk kivágás-beszúrás műveletet. Írj programot (MOZGAT.PAS, MOZGAT.C vagy MOZGAT.CPP néven), amely kiszámítja, hogy

a) a szöveg első 10 sora hova került a műveletek elvégzése után;
b) az eredeti szöveg mely sorai kerültek az első 10 sorba a műveletek hatására.

Bemenet:

A MOZGAT.BE állomány első sora két (szóközzel elválasztott) egész számot tartalmaz: az első a szöveg sorainak a száma, N (10<=N<=1000000), a második pedig a műveletek száma, K (1<=K<=1000). A további K sor mindegyikében (egy-egy szóközzel elválasztva) három egész szám van: A, B és C, amelyek egy-egy műveletet írnak le. A számokra teljesülnek a következő egyenlőtlenségek: 1<=A<B<=N, továbbá 0<=C<A vagy B<=C<=N. Ha C=0, akkor a kivágott szöveget az első sor elé kell beszúrni.

Kimenet:

A MOZGAT.KI állomány két sorába 10-10 számot kell írni egy-egy szóközzel elválasztva. Először azoknak a szövegsoroknak a sorszámát kell felsorolni, ahová az eredeti szöveg első 10 sora került a műveletek hatására. Azután az eredeti szöveg azon sorainak a sorszámát kell felsorolni, amelyek a műveletek hatására az első 10 sorba kerültek át.

Példa:

3. feladat: Ütemezés (15 pont) /tesztadatok/

Mekk Elek ezermester népszerű vállalkozó, sokan keresik fel megrendelésekkel. Minden megrendelt munkának ismeri a kezdési és a befejezési idejét. A mester a következő évre szóló megrendelések közül a lehető legtöbbet akarja elvállalni, de egyszerre csak egy munkán tud dolgozni.

Feladat:

Írj programot (UTEMEZ.PAS, UTEMEZ.C vagy UTEMEZ.CPP néven), amely meghatározza a munkák egy lehető legnagyobb elemszámú részhalmazát úgy, hogy az összes kiválasztott munka elvégezhető legyen.

Bemenet:

Az UTEMEZ.BE állomány első sora a megrendelések N számát (1<=N<=10000) tartalmazza. A következő N sor mindegyike két pozitív egész számot tartalmaz, a megrendelt munka K kezdési, illetve B befejezési idejét (1<=K<=B<=365), tehát a J-edik munkát az állomány J+1-edik sora írja le.

Kimenet:

Az UTEMEZ.KI állomány első sorában a kiválasztott munkák M száma legyen. A második sorba M számot, a kiválasztott munkák sorszámát kell írni egy-egy szóközzel elválasztva, tetszőleges sorrendben. Ha több megoldás is van, közülük egy tetszőlegeset kell kiírni.

Példa:

4. feladat: Tükörszó (20 pont) /tesztadatok/

Egy szót tükörszónak nevezünk, ha balról és jobbról kiolvasva betűről betűre megegyezik. (Tehát minden egybetűs szó tükörszó.) Minden szóban található tükörszó, amin azt értjük, hogy ha kitörlünk belőle betűket, akkor tükörszót kapunk.

Feladat:

Írj programot (TUKOR.PAS, TUKOR.C vagy TUKOR.CPP néven), amely meghatározza egy adott szóban található leghosszabb tükörszó hosszát!

Bemenet:

A TUKOR.BE állomány egyetlen sorában egy legfeljebb 100 karakterből álló S szó van.

Kimenet:

A TUKOR.KI állományba egyetlen számot kell írni: az S szóban található leg-hosszabb tükörszó hosszát.

Példa:

Elérhető összpontszám: 75 pont + 25 pont az 1. fordulóból