Nemes Tihamér OKSzTV'2001
Második forduló
11-13. osztályosok
2001. január 20. 900-1400
1. feladat:
Jégtömb (20 pont) /tesztadatok/
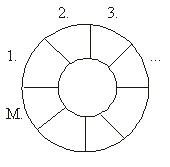
Jégtömböket írunk le egy táblázat segítségével. A szürkével
jelölt pontok jelölik a jégtömbbe tartozó pozíciókat. Ha a jégtömbre meleg
levegőt fújunk, akkor a szélén olvadni kezd, s a keletkezett víz elfolyik.
Az olvadás szabálya: egy időegység alatt abban a mezőben levő jég olvad
el (s tűnik el a táblázatból), amelynek 4 oldalszomszédja közül legalább
2 levegő volt. (Ilyenek az ábrán 1-es számmal jelölt pontok.) Ezután keletkezhetnek
újabb ilyen tulajdonságú pontok (az ábrán 2-vel jelöljük őket). amelyek
a 2. időegységben olvadnak el és így tovább.

Általánosítsuk ezt a problémát 3 dimenziósra, álljon a táblázat K darab
ilyen egymás fölötti síkból (azaz a négyzetek helyett kockákkal dolgozunk)!
Ekkor a mezőben levő jég akkor olvad el, ha a mező 6 lapszomszédja közül
legalább 3-ban levegő van.
Feladat:
Készíts programot, (JEGTOMB.PAS vagy JEGTOMB.C), amely egy
adott 3-dimenziós jégtömbre megadja, hogy hány időegység alatt olvad el
teljesen, illetve időegységenként megadja, hogy a jégtömb még hány mezőből
áll.
Bemenet:
A JEGTOMB.BE állomány első sorában három egész szám van, egy-egy
szóközzel elválasztva, a "táblázat" sorainak (1<=N<=40), oszlopainak
(1<=M<=40) és síkjainak (1<=K<=40) a száma. Ezt követi a K
darab sík leírása. Minden síkhoz N sor tartozik, amelyek mindegyike M számot
tartalmaz, közülük az i-edik sor j-edik szánjegye 0, ha az adott sík i-edik
sorának j-edik oszlopában levegő van, és 1, ha jég. A "táblázat" szélső
mezőiben biztosan levegő van.
Kimenet:
A JEGTOMB.KI állomány első sorába azon időegységek T számát
kell írni, ami alatt a jég teljesen elolvad. A következő T sorba egy-egy
számot kell írni, közülük az i-edik a jéggel teli mezők száma legyen az
i-edik időegység kezdetén! (A legutolsó időegység után már 0 a jéggel teli
mezők száma, ezt az állományba nem szabad kiírni.)
Példa:
| JEGTOMB.BE |
JEGTOMB.KI |
4 5 4
00000
00000
00000
00000
00000
01110
01110
00000
00000
01110
01110
00000
00000
00000
00000
00000 |
2
12
4 |
2. feladat:
Licit (20 pont) /tesztadatok/
Nevesincs sziget polgármestere elhatározta, hogy értékesíti
a sziget tengerpartját. A partot egyforma méretű parcellákra osztotta.
A polgármester úgy döntött, hogy a parcellákat nyilvános pályázat keretében
adja el, azaz egy adott határidőig minden érdeklődő lezárt borítékban leadhatja
ajánlatát. Egy pályázó csak egy ajánlatot nyújthat be, amelyben meg kell
adnia, hogy melyik parcellától melyik parcelláig terjedő részt kívánja
megvenni, és mennyiért.
A pályázat sikeres volt, a határidő lejártáig N pályázat érkezett. Ezek
közül ki kell választani azokat az ajánlatokat, amelyek a legtöbb bevételt
eredményezik, s persze úgy, hogy egyetlen parcellát sem ítélünk oda egynél
több pályázónak. Egy-egy pályázó vagy az összes kért parcellát megkapja,
vagy egyet sem kap meg. Előfordulhat, hogy a maximális bevétel eléréséhez
nem kell eladni az összes parcellát.
Feladat:
Írj programot (LICIT.PAS vagy LICIT.C), amely megadja a választ
a polgármester problémájára!
Bemenet:
A LICIT.BE állomány első sorában a pályázatok N száma (1<=N<=100)
és a parcellák M száma (1<=M<=100) található, egy szóközzel elválasztva.
A következő N sor az egyes pályázók adatait tartalmazza, a pályázókat ez
a sorrend azonosítja. Mindegyik 3 számot tartalmaz egy-egy szóközzel elválasztva:
A B FT, ami azt jelenti, hogy a pályázó az A sorszámú parcellától (1<=A<=M)
a B sorszámú parcelláig (1<=B<=M) terjedő részért FT forintot fizetne
(1000<=FT<=1000000). Ha B<A, akkor a pályázó A-tól M-ig és 1-től
B-ig szeretné megvásárolni a parcellákat.
Kimenet:
A LICT.KI állomány első sorába az elérhető legnagyobb bevételt
kell írni. A második sorba azon páláyzók sorszámai kerüljenek egy-egy szóközzel
elválasztva, akik nyerése esetén érhető el a legnagyobb bevétel. Ha több
megoldás is lenne, akkor közülük csak egyet kell kiírni (bármelyiket).
Példa:
| LICIT.BE |
LICIT.KI |
5 6
1 5 10000
2 3 5000
4 5 5000
4 4 6000
6 1 3000 |
14000
2 4 5 |
3. feladat:
Hálózat (15 pont) /tesztadatok/
Egy hírközlési hálózat csomópontokból és csomópont-párokat
összekötő vezetékekből áll. Egy csomópont-pár tagjait közvetlenül összekötő
vezetékek kétirányú kapcsolatot tesz lehetővé a két pont között. E két
csomópont közötti adatátvitel sebességét a vezeték sávszélességének nevezzük.
Két adott pont között az adatátvitelt közvetlennek nevezzük, ha a két pont
össze van kötve vezetékkel, és közvetettnek, ha az adatok közbeiktatott
csomópontokon is áthaladnak. A két tetszőleges pont közötti útvonal átviteli
sebessége a közbeiktatott vezetékek sávszélességének minimuma. Bármely
két csomópont között legfeljebb egy vezeték van, azonba több közvetett
összeköttetés is létezhet közöttük.
Feladat:
Készíts olyan programot (HALOZAT.PAS vagy HALOZAT.C), amely
kiszámítja a hálózat két adott csomópontja között a legnagyobb adatátviteli
sebességet nyújtó útvonal sávszélességét!
Bemenet:
A HALOZAT.BE szöveges állomány első sora három egész számot
tartalmaz egy-egy szóközzel elválasztva (N A B). N (2<=N<=100) a
csomópontok száma, A és B (1<=A<=N, 1<=B<=N, A<>B) a két
kijelölt csomópont. A csomópontokat 1 és N közé eső természetes számokkal
azonosítjuk. A második sorban egyetlen egész szám van, a közvetlenül összekötött
csomópontpárok M (1<=M<=10000) száma. A következő M sor mindegyikében
három egész szám van egy-egy szóközzel elválasztva: X Y S. X és Y a két
közvetlenül összekötött csomópont azonosítója (1<=X<=N, 1<=Y<=N,
X<>Y), S (1<=S<=1000) pedig az X-et az Y-nal összekötő vezetékek
sávszélessége.
Kimenet:
A HALOZAT.KI állomány egyetlen sorába egy egész számot kell
írni: a kijelölt A és B csomópontok közötti legnagyobb sávszélességet.
Ha a két csomópont között nincs út, akkor 0-t kell kiírni.
Példa:
| HALOZAT.BE |
HALOZAT.KI |
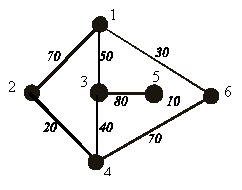
6 1 6
8
1 2 70
1 3 50
1 6 30
2 4 20
3 4 40
3 5 80
4 6 70
5 6 10 |
40 |
4. feladat:
Gén (20 pont) /tesztadatok/
A genetikai kód egyértelműem leírható a négyféle bázis (adenin,
citozin, guanin, timin) sorrendjével. A bázisokat a kezdőbetűjükkel (A,
C, G, T) jelöljük. Óriásmolekulák bázisszekvenciáját nehéz meghatározni,
ezért a vizsgálat előtt az óriásmolekulát megfelelő enzimekkel feldarabolják
kisebb (rövidebb) molekuladarabokra. Ugyanazt az óriásmolekulát többféleképpen
is feldarabolják, azt azonban nem lehet tudni, hogy a keletkező kisebb
molekulák melyik darabolásból származnak. Tudjuk viszont, hogy (1) a molekuladarabok
különböznek egymástól, (2) minden molekuladarab csak egy helyre illeszthető
be az óriásmolekulába, (3) ugyanazon helyen legfeljebb egyszer vágjuk el
az óriásmolekulát.
A feldarabolás után kémiai módszerekkel meghatározzák a keletkezett
molekuladarabok bázissorrendjét.
Az egyes darabok csak a leírt sorrendben használhatók fel, megfordítani
nem szabad őket!
Feladat:
Készíts programot (GEN.PAS, GEN.C), amely a molekuladarabok
bázissorrendjéből előállítja az eredeti óriásmolekula bázissorrendjét!
Bemenet:
A GEN.BE állomány első sorában a feldarabolások száma (2<=K<=10)
és egy szóközzel elválasztva a keletkezett molekuladarabok száma (1<=N<=100)
található. A következő N sor mindegyike egy 10-25 karakterből álló betűsorozatot
tartalmaz, az egyes molekuladarabok bázissorrendjét.
Kimenet:
A GEN.KI egyetlen sorába egy legfeljebb 250 karakterből álló
szöveget kell írni, az eredeti óriásmolekula bázissorrendjét. Ha több megoldás
is lenne, akkor azok közül csak egyet kell kiírni (bármelyiket).
Példa:
(A karaktersorozatok hossza itt az érthetőség miatt kisebb,
mint a feladatban megadott minimális határ)
| GEN.BE |
GEN.KI |
2 5
AACG
AAC
AGT
GA
GT |
AACGAGT |
Elérhető összpontszám: 75 pont + 25 pont az 1. fordulóból


