Nemes Tihamér OKSzTV 2002

1. feladat: Válogatós (26 pont)

Lányok (N) és fiúk (M) ülnek egy sorban, vegyesen (N+M>0). Szeretnénk úgy ültetni őket, hogy az első N széken üljenek a lányok, a következő M széken pedig a fiúk.

A feladat megoldására a következő algoritmust találtuk ki:

1. Az első széken levőt felállítjuk (kezdetben ez lesz a szabad szék).
2. Az utolsó széktől visszafelé, de legfeljebb a szabad székig haladva keresünk egy lányt.
3. Ha találunk, akkor megjegyezzük, hogy legközelebb már csak innentől kezdve kell lányt keresni, és a lányt átültetjük a szabad székre.
4. Ezután az első széktől, de legfeljebb a szabad székig haladva keresünk egy fiút.
5. Ha találunk, akkor megjegyezzük, hogy legközelebb már csak innentől kezdve kell fiút keresni, és a fiút átültetjük a szabad székre.
6. Ha egyik keresés során sem értük el a szabad széket, akkor a 2. ponttól kezdve foly-tatjuk a keresést.
7. A szabadon maradt székre ültetjük azt, akit az első lépésben felállítottunk.

Példa: (Dóra,Endre,Ágnes,István) => (-,Endre,Ágnes,István) => (Ágnes,Endre,-, István) => (Ágnes,-,Endre,István) => (Ágnes,Dóra,Endre,István)

A. Mi lesz az eredmény, ha kezdetben a székeken ülők sorrendje (azaz a kezdő ülésrend): (Erika,János,Nóra)? A fenti példához hasonlóan lépésenként írd le!
B. Mi lesz az eredmény, ha a kezdő ülésrend: (Anna, Emese, Béla, Enikő, András, Jakab, Eszter, Móni, László, Piri, Péter)? A fenti példához hasonlóan lépésenként írd le!
C. Van olyan kezdő ülésrend, hogy csak egyetlen gyereknek kell mozognia. Melyik gyereknek, milyen kezdő ülésrend esetén?
D. Van olyan kezdő ülésrend, hogy minden gyereknek mozognia kell. Melyik ez a kezdő ülésrend?

Egy kockajátékot négy dobókockával játszanak. A dobás után összeszámolják, hogy a négy kocka közül hány mutat egyforma számot.

A lehetőségek:

Egy pár: két szám egyforma, a másik kettő tőlük és egymástól is különböző (pl. 3,1,3,5).
Két pár: két-két szám egyforma, de a párok egymástól különbözők (pl. 2,4, 4,2).
Terc: három szám egyforma, a negyedik tőlük különböző (pl. 6,6,1,6).
Póker: mind a négy szám egyforma (pl. 5,5,5,5).
Semmi: mind a négy szám különböző (pl. 1,6,2,5).


Az alábbi algoritmus az A,B,C,D változók értéke alapján kiírja, hogy milyen dobásunk volt (segítség: az algoritmusban minden elágazásnak van "akkor" és van "különben" ága is).

Mit kell írni a ?1 … ?15 helyébe, hogy a helyes eredményeket kapjuk meg?
 

Póker(A,B,C,D):   Ha A=B akkor  Ha C=D akkor  Ha A=D akkor  Ki: ?1                                    különben Ki: ?2                       különben ha A=C akkor  Ki: ?3                                különben ha B=D akkor Ki: ?4                                különben Ki: ?5         különben ha C=D akkor  Ha A=C akkor Ki: ?6                                különben ha B=D akkor Ki: ?7                                különben Ki: ?8                       különben ha A=C akkor Ha B=D akkor  Ki: ?9                                                    különben Ki:?10                                különben ha A=D akkor  Ha B=C akkor  Ki: ?11                                                              különben Ki: ?12                                különben ha B=D akkor Ki: ?13                                         különben ha B=C akkor Ki: ?14                                         különben Ki: ?15  Eljárás vége.

Egy pénztárban hatféle bankjegyet (címletet) kezelnek.  Az alábbi címletező algoritmus, szándékunk szerint, meghatározza, hogy a P összeg hogyan fizethető ki a lehető legkevesebb bankjeggyel. Az eredményt a DB vektor tartalmazza. Minden címletből korlátlan mennyiség használható fel.
 

Címletezés(P,C,DB):   K:=6; DB:=(0,0,0,0,0,0)   Ciklus amíg P>0     Ciklus amíg P>=C(K)       DB(K):=DB(K)+1; P:=P-C(K)     Ciklus vége     K:=K-1   Ciklus vége Eljárás vége.

Ez az algoritmus például a C=(1,2,5,10,20,50) címletkészlet és 96 forint kifizetése esetén a DB=(1,0,1,0,2,1) vektort állítja elő.

Legyenek a címletkészletek a következők:

 i) C=(1,3,6,10,60,100)
ii) C=(1,4,6,10,40,60)
iii) C=(1,2,5,12,60,120)
iv) C=(1,5,7,21,35,49)

A. Mi lesz a DB vektor értéke 73 forint kifizetésekor a négy címletkészlet esetén?
B. A négy címletkészlet közül melyeknél címletez hibásan az algoritmus (azaz nem a lehető legkevesebb bankjegyet használja fel)?
C. Minden hibás eredményhez vezető címletkészletre add meg azt a legkisebb P összeget, amelynek a kifizetésére az algoritmus nem a lehető legkevesebb bankjegyet használja fel! Add meg az algoritmus által előállított hibás, valamint a helyes DB vektort is!

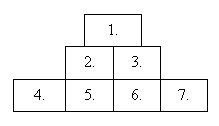Dobozokból piramist építünk. A piramis minden szintjén (az alsót kivéve) pontosan kétszer annyi doboz van, mint a felette levő szinten. A dobozokat az ábra szerint sorszámozzuk.

Definíció:

• Az I sorszámú doboz alatti doboznak a 2*I és a 2*I+1 sorszámút nevezzük, az I sorszámú doboz feletti doboznak pedig az I div 2 sorszámút.
• A következő algoritmust hajtjuk végre N darab egész számmal. Kezdetben a dobozok üresek. Az első számot az 1 sorszámú dobozba tesszük. Ha már I-1 darab számot felhasználtunk, akkor az I-edik számot az I sorszámú dobozba tesszük, majd összehasonlítjuk a felette levővel; ha nagyobb nála, akkor felcseréljük a dobozok tartalmát. A csere után a számot ismét összehasonlítjuk a felette levővel, és ha nagyobb nála, ismét cserélünk és így tovább.


Feljegyzések:
A. Add meg a piramis állapotát (azaz a dobozok tartalmát) minden lépés után, ha a bemenő számsorozat: (7,2,9,5,1,3,8)!
B. Fogalmazd meg általánosan, hogy milyen tulajdonságú szám lesz az algoritmus befejeződésekor a piramis tetején!
C. Fogalmazd meg általánosan, hogy milyen viszonyban van az algoritmus végrehajtása után az I sorszámú dobozban levő szám a fölötte és az alatta levőkkel (feltéve, hogy van szám fölötte, illetve alatta)!

Elérhető összpontszám: 100 pont