Nemes Tihamér OKSzTV 2001

1. feladat: Mókusok (28 pont)

Mókusok télire diót és mogyorót gyűjtenek az erdőben (N darabot). Amit találnak, azt lyukakba rejtik, egy lyukba egyet. A főmókus szeretné ésszerűen elrendezni a gyűjteményt, s ezért az alábbi algoritmus alapján rendezi át a diók és mogyorók sorrendjét:
 

Eljárás:   i:=1; j:=N; Tedd zsebre az 1. lyukban levő valamit!   Ciklus amíg i<j     Ciklus amíg i<j és a j. lyukban mogyoró van       j:=j-1     Ciklus vége     Ha i<j akkor Tedd át a j. lyukból az i. lyukba!     Ciklus amíg i<j és az i. lyukban dió van       i:=i+1     Ciklus vége     Ha i<j akkor Tedd át az i. lyukból a j. lyukba!   Ciklus vége   Tedd a zsebedből az i. lyukba! Eljárás vége.

A. Milyen sorrendben lesznek az algoritmus végén a diók és mogyorók?
B. Az algoritmus alapján hogyan lehetne megmondani, hogy hány diót, illetve hány mogyorót gyűjtöttek?
C. Az algoritmus milyen elhelyezkedésű diókat, illetve mogyorókat hagy a helyén?
D. Add meg, hogy legjobb, illetve legrosszabb esetben hány gyümölcsöt (diót és mogyorót) kell mozgatni és milyen ekkor a kezdeti elrendezés?

Egy szobanövény az elültetése utáni évben két zöld levelet növeszt. A második évben 2 piros levelet, majd a harmadik évben elágazik kétfelé. A negyedik évtől kezdve az új ágakon ugyanaz történik, mint az eredeti növényen, azaz megjelenik két zöld levél, egy évre rá két piros levél, majd újabb 1 év múlva ezek az ágak is szétágaznak kétfelé. (Mint az ábrán látszik, az 1 éves növénynek 2 levele van, a 2 és a 3 évesnek 4, …)



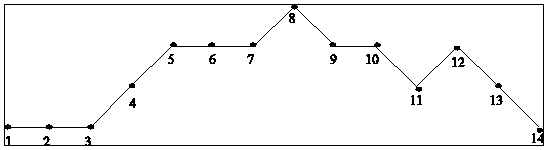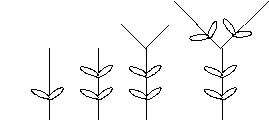
A. Hány piros levele lesz a 6 éves növénynek? (A 3 évesnek 2 van.)
B. Hány zöld levele lesz a 7 éves növénynek? (A 3 évesnek 2 van.)
C. Hány ágvége lesz összesen a 8 éves növénynek? (A 3 évesnek 2 van.)
D. Hányadik évben lépi túl a levelek száma a 200-at?
E. Milyen években lesz a növénynek több zöld levele, mint piros?

Egy hegymászó az útja során N pontban feljegyezte, hogy milyen tengerszint feletti magasságban járt. Ezt mutatja az ábra. Az i-edik pontban mért tengerszint feletti magas-ságot X_i-vel jelöljük. Az egyes pontok különböző nehézségű szakaszok határán vannak (pl. emelkedő, sík, …). Az alábbi algoritmus ezeket sorolja be 3 csoportba:
 

Pontok:   Ciklus i=2-től N-1-ig     Ha (Xi-Xi-1)*(Xi+1-Xi)>0 akkor Ki: i,’ 1. típusú’ {*}     Ha (Xi-Xi-1)*(Xi+1-Xi)=0 akkor Ki: i,’ 2. típusú’ {**}     Ha (Xi-Xi-1)*(Xi+1-Xi)<0 akkor Ki: i,’ 3. típusú’ {***}   Ciklus vége Eljárás vége.

A. Az ábrán látható pontok közül milyen sorszámúakat sorol be az algoritmus az 1, 2, illetve 3 típusú pontok közé?

Az i-edik pontban mért tengerszint feletti magasságot Xi-vel jelöljük. Az egyes pon-tok különböző nehézségű szakaszok határán vannak (pl. emelkedő, sík, …). Az alábbi algoritmus ezeket sorolja be 3 csoportba:

A *-gal jelölt kiírások helyére újabb algoritmusrészleteket teszünk a pontok további osztályozása érdekében:
 

{*}:    Ha (Xi-Xi-1) >0 akkor Ki: i,’ 1/A típusú’                    különben Ki: i,’ 1/B típusú’

{**}:    Elágazás      (Xi-Xi-1)>0 esetén Ki: i,’ 2/A típusú’      (Xi+1-Xi)>0 esetén Ki: i,’ 2/B típusú’      (Xi-1-Xi)>0 esetén Ki: i,’ 2/C típusú’      (Xi-Xi+1)>0 esetén Ki: i,’ 2/D típusú’      egyéb esetben Ki: i,’ 2/E típusú’    Elágazás vége

{***}:     Ha (Xi-Xi-1)>0 akkor akkor Ki: i,’ 3/A típusú’    különben Ki: i,’ 3/B típusú’

B.

Az ábrán látható pontok közül milyen sorszámúakat sorol be az algoritmus az 1/A, 1/B, …, 3/B típusú pontok közé?

Osztályod két bulit rendezett. A rendezvényre az osztálytársak különböző időpontokban érkeztek, illetve távoztak. Valaki pontosan feljegyezte minden résztvevő tanulóról, hogy az mikor érkezett, illetve távozott. Egy feljegyzés egy [a,b] számpár, ami azt jelenti, hogy a tanuló az a időponttól a b időpontig volt jelen a rendezvényen (beleértve az a és a b időpontokat is). Minden időpont a rendezvény kezdete óta eltelt idő másodpercben mérve.

Feljegyzések:
 

1. [600, 1000], [1, 100], [100, 500], [500, 700], [400, 800], [650, 900], [300, 600], [66, 120]

2. [1, 1000], [4000, 6000], [500, 2113], [2345, 5000], [601, 1000], [5000, 6000], [2000, 3000], [2345, 3333], [3001, 4000], [3350, 5010], [4001, 5000], [6300, 9000], [5056, 5156], [5621, 6000], [3350, 5056], [6000 7000]

A. Hányan voltak legtöbben egyszerre jelen a rendezvényen?
B. Adj meg egy olyan időpontot, amikor a legtöbben voltak egyszerre jelen.
C. Legalább hány fényképet kellett volna készíteni ahhoz, hogy mindenki szerepeljen legalább egy fényképen?
D. Adj meg a C. kérdésben szereplő számú időpontot, hogy ha ekkor készült volna egy-egy fénykép, akkor mindenki szerepelne legalább egy fényképen.

Elérhető összpontszám: 100 pont