

Évszázadokkal ezelőtt Artúr király és a Kerekasztal lovagjai minden újévkor ünnepélyes baráti találkozót tartottak. A találkozók emlékére egyszemélyes táblajátékot készítettünk. A játékot olyan táblán játsszák, amelynek különböző mezőire egy Királyt és több Lovagot helyezünk el véletlenszerűen.A Tábla egy 8x8-as négyzetrács.
A Király a következő ábrának megfelelően léphet a
mezőről a
mezőkre, de természetesen nem léphet le a tábláról.
A Lovag az alábbi ábrának megfelelően léphet a
mezőről a
mezőkre, de természetesen nem léphet le a tábláról.
A játék során ugyanarra a mezőre egyszerre több bábu is léphet.
A játék célja, hogy az összes bábu egy mezőre kerüljön, a lehető legkevesebb lépésben. A fenti szabályokon kívül a következő lépésszabály is alkalmazható: Ha a Király és egy Lovag ugyanarra a mezőre lépett, akkor ezt követen a Király és a Lovag együtt, Lovagként haladhat tovább. Ebben az esetben a Király és a Lovag közös lépése egy lépésnek számít.Feladat:
Írj programot, amely kiszámítja azt a minimális lépésszámot, amellyel az összes bábu egy mezőre vihető.Bemenet:A CAMELOT.IN állomány egyetlen sorában a kezdeti táblaállás van, stringként kódolva.Kimenet:
A string legfeljebb 64 különböző mezőn levő bábu pozícióját tartalmazza, amelyek közül az első a Királyé, a többi pedig a Lovagoké. Minden pozíciót egy betű-számjegy pár ad meg. A betű a vízszintes, a számjegy pedig a függőleges koordinátát jelöli, a sorban egyetlen szóköz sincs. (Tehát a lovagok száma legfeljebb 63.)A CAMELOT.OUT állományba egyetlen sort kell írni, amely a minimális lépésszámot tartalmazza.Példa:
INPUT OUTPUT D4A3A8H1H8 10
Egy falra téglalap alakú képeket helyeznek el, amelyek oldalai vízszintesek, illetve függőlegesek. A képeket egymásra is rakhatják, így azok részben vagy teljesen lefedhetik egymást. A téglalapok egyesítését határoló (külső vagy belső) vonalak hosszát nevezzük kerületnek.Feladat:
Írj programot, amely kiszámítja a kerületet.Bemenet:Az alábbi ábrán 7 téglalap látható.
A téglalapok egyesítését határoló vonalakat mutatja a következő ábra.
A következő N sor mindegyike egy-egy téglalap bal alsó és jobb felső sarkának koordinátáit tartalmazza. Minden sorban először a bal alsó sarok x-, utána az y-koordinátája, majd a jobb felső sarok x-, utána pedig az y-koordinátája van.
A koordináták egész számok.A PICTURE.OUT állomány egyetlen sorába egy nemnegatív egész számot kell írni: a kerületet.Korlátok:0<= téglalapok száma < 5000Példa:
Minden koordináta értéke a [-10000,10000] tartományba esik.
A téglalapok egyik oldala sem lehet 0 hosszúságú.
Az eredmény kiszámítása 32-bites előjeles egész számokat igényelhet.
PICTUTE.IN PICTURE.OUT 7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16228
A Polygon olyan egyszemélyes játék, amelyet egy N csúcsú sokszögön játszanak. Az 1. ábra olyan példát mutat, ahol N=4. Címkeként minden csúcshoz egy egész számot, az élekhez pedig a + (összeadás) vagy a * (szorzás) jelét rendeljük. Az N darab élt 1-től N-ig sorszámozzuk.
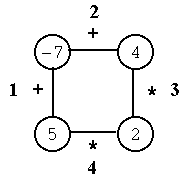
Az ábra a Polygon játék egy kezdőállását mutatja.Első lépésként egy tetszőleges élt távolítunk el.
A következő lépések mindegyike az alábbiakból áll:
A játék akkor ér véget, ha elfogytak az élek, azaz egyetlen csúcs maradt. A játék eredménye a megmaradt egyetlen csúcshoz tartozó érték.
- kiválasztunk egy E élt, amely a V1 és a V2 csúcsot köti össze; majd
- a V1 és a V2 csúcsot egy új csúccsal helyettesítjük, ennek címkéjét úgy kapjuk, hogy az E élhez rendelt műveletet végrehajtjuk a V1 és a V2 csúcsokhoz rendelt értékekkel.
Példa a játékra:
Az előző ábrán látható sokszögből a játékos először a 3 élt veszi el. Ennek hatása a következő ábrán látható.Feladat:
Ezután a játékos az 1 élt választja:
Ezután a játékos a 4 élt választja:
Végül a 2 élt választja. Az eredmény 0 lesz.
A második sor adja meg az élek sorszámának sorrendjében az 1, ..., N élek címkéit, és két egymást követő él címkéje között a köztük levő csúcs címkéjét. Az 1 és 2 él között van az 1. csúcs címkéje, a 2 és 3 él címkéje között a 2. csúcsé, és így tovább, legvégül az N él címkéje után van a N. csúcs címkéje. Az élek és csúcsok címkéit egy-egy szóköz választja el.
Az élek címkéjeként összeadás (+) esetén a t, szorzás (*) esetén az x karaktert használjuk.A POLYGON.OUT állomány első sorába a játékban elérhető legnagyobb eredményt kell írni. A második sorba azoknak az éleknek a sorszá-mát kell írni, amelyeket valamely játszmában első lépésként eltávolítva elérhető a maximális eredmény. A sorszámokat növekvő sorrendben, egy-egy szóközzel elválasztva kell kiírni.Korlátok:3<= N<= 50Példa:
A csúcsokhoz rendelt értékek bármely lépésben a [-32768,32767] tartományban vannak.
POLYGON.IN POLYGON.OUT t -7 t 4 x 2 x 5 33
1 2