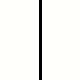Nemes Tihamér OKSzTV 2002

Egy építkezés befejezéséhez N különböző  munkát kell elvégezni. Minden munka pontosan egy nap alatt teljesíthető. A terv alapján tudjuk, hogy bizonyos munkákat előbb kell elvégezni, mint másokat. Pontosabban, a terv (A, B) párok halmazát tartalmazza, ahol az (A, B) pár azt jelenti, hogy az A munkát előbb kell elvégezni, mint a B munkát.  Vannak olyan speciális munkák is, amelyekből egy nap csak egy végezhető el, ráadásul csak a megadott sorrendben (de nem feltétlenül egymást követő napokon).

Feladat:

Írj programot, (EPITKEZ.PAS, EPITKEZ.C vagy EPITKEZ.CPP), amely

A. kiszámítja, hogy legkevesebb hány nap kell az összes munka elvégzéséhez;
B. megadja a munkáknak egy olyan beosztását, amely szerint minden munka a lehető legkorábban végezhető el a követelmények teljesülése mellett.

Bemenet:

Az EPITKEZ.BE állomány első sora az N, K és T egész számokat tartalmazza. N az elvégzendő munkák száma (1<=N<=200), az egyes munkákat az 1, ..., N számokkal azonosítjuk. K (1<=K<=N) a speciális munkák száma. A T tervben megadott megelőzési párok száma (1<=T<=10000). A második sor pontosan K egész számot tartalmaz egy-egy szóközzel elválasztva, minden szám egy-egy speciális munka sorszáma. A további T sor mindegyikében két egész szám van: A, B (1<=A<=N, 1<=B<=N), ami azt jelenti, hogy az A munkát előbb kell elvégezni, mint a B-t.

Kimenet:

Az EPITKEZ.KI állomány első sorába egy egész számot kell írni: annak a lehető legrövidebb időnek a napokban mért hosszát, amely alatt az összes munkát el lehet végezni. Ezt követően az állományban pontosan M sornak kell lennie. Az állomány (i+1)-edik sora azon munkák sorszámát tartalmazza, egy-egy szóközzel elválasztva, amelyeket legkorábban az i-edik napon lehet és kell elvégezni. Ha nem lehet a tervben megadott feltételeket teljesíteni, akkor az első sorba 0-t kell írni.

Példa:

EPITKEZ.BE	EPITKEZ.KI
10 3 11 1 2 8 1 3 3 4 1 5 5 3 3 7 5 6 1 8 8 6 6 9 9 10 7 10	6 1 2 5 8 3 6 4 7 9 10

Adott egy nagy színes raszteres kép (N*N méretű) futamhossz kódolással, adott továbbá egy kis raszteres kép kódolatlanul (K*K méretű). Futamhossz-kódoláskor a képet sorokra bontjuk, s minden sort számpárok sorozatával írunk le. A számpár első tagja egy darabszám, a második tagja pedig egy színkód (0 és 255 közötti egész szám), a jelentése pedig: ennyi darab ilyen színű pontot kell egymás mellé tenni. (Például az 1 1 1 1 1 2 2 2 1 1 színkódokat tartalmazó sor futamhossz-kódja: 5 1 3 2 2 1.)

Feladat:

Készíts programot (KEP.PAS, KEP.C vagy KEP.CPP), amely a nagy képben megkeresi a kis kép első előfordulását (fentről lefelé, balról jobbra haladva)!

Bemenet:

A NAGYKEP.BE állomány első sorában a nagy kép sorainak és oszlopainak a száma (N) van megadva (1<=N<=1000), a következő N sorban pedig a kép egyes sorait leíró futamhossz-kódok (soronkén legfeljebb 100 számpár), a számokat egymástól egy-egy szóköz választja el.
A KEP.BE állomány első sorában a kis kép sorainak és oszlopainak a száma (K) van megadva (1<=K<=100), a következő K sor mindegyike K egész számot, az egyes képpontok színkódját tartalmazza egy-egy szóközzel elválasztva.

Kimenet:

A KEP.KI állomány egyetlen sorába két egész számot kell írni, SOR-t és OSZLOP-ot, a kis kép első előfordulási pozíciójának a koordinátáit a nagy képen belül (1<=SOR<=N-K+1, 1<=OSZLOP<=N-K+1), egy szóközzel elválasztva. Ha a nagy kép nem tartalmazza a kis képet, akkor SOR és OSZLOP legyen 0!

Példa:
 

NAGYKEP.BE	KEP.BE	KEP.KI
20 20 1 5 1 5 2 5 1 5 2 11 1 1 2 1 3 1 4 1 5 5 2 5 1 5 2 2 1 8 2 5 2 8 1 7 2 11 1 9 2 20 1 20 1 20 1 20 1 20 1 20 1 20 1 20 1 20 1 20 1 20 1 20 1 20 1 20 1	5 1 1 1 1 1 1 2 3 4 5 1 1 2 2 2 1 1 1 2 2 1 2 2 2 2	2 11

Egy négyzetrácsos hálózat mezőin elhelyezett tárgyakat egy robotnak kell összegyűjtenie. A robot a bal felső sarokból indul, amelynek (1, 1) a koordinátája, és a jobb alsó sarokba kell érkeznie, amely az (N, N) koordinátájú mező. A robot elemi parancsok sorozatából álló programot tud végrehajtani. Három elemi robotparancs van:

• J: jobbra lép a szomszédos mezőre ( (sor, oszlop)-ról (sor, oszlop+1)-re ),
• L: lefelé lép a szomszédos mezőre ( (sor, oszlop)-ról (sor+1, oszlop)-ra ),
• F: felfelé lép a szomszédos mezőre ( (sor, oszlop)-ról (sor-1, oszlop)-ra ).

A robot nem tud visszafordulni, azaz a programban L után közvetlenül nem állhat F, és F után közvetlenül nem állhat L.

Feladat:

Írj programot (ROBOT.PAS, ROBOT.C vagy ROBOT.CPP), amely

1. kiszámítja, hogy a robot legkevesebb hány lépés megtételével tudja összegyűjteni a tárgyakat;
2. megad egy olyan robotprogramot a tárgyak összegyűjtésére, amely a lehetséges legkevesebb lépést tartalmazza!

Bemenet:

A ROBOT.BE állomány első sora az N és K egész számokat tartalmazza: N a négyzetrácsos hálózat mérete (1<=N<=1000), K pedig a mezőkön található tárgyak száma (1<=K<=100000). A további K sor mindegyikében két egész szám van: X, Y egy olyan mező koordinátái, ahol a tárgy van elhelyezve (1<=X<=N, 1<=Y<=N).

Kimenet:

A ROBOT.KI állományba két sort kell írni. Az első sor a lehetséges legkevesebb lépés számát (M) tartalmazza, amellyel a robot összegyíjtheti a tárgyakat. A második sor egy olyan robotprogramot írjon le, amelynek végrehajtásával a robot elvégzi a munkát. A sor pontosan M betűből álljon, ahol minden betű egy lehetséges robotparancs jele (J, L vagy F) lehet. A betűk között nem lehet szóköz.

Példa:
 

ROBOT.BE	ROBOT.KI
8 10 2 2 3 2 5 2 1 5 1 6 3 4 3 6 5 5 6 4 7 6	28 JLLLLJFFJLLLJFFFFFJLLLLLLJJL

Egy négyzetrácsos szerkezetű városban villamosok közlekednek. A villamospályákat egy térképpel írjuk le, ahol minden térképelem egy-egy négyzet alakú pályaelemnek felel meg. A következő pályaelemek vannak:
 

0:	1:	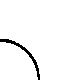2:	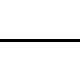3:
4:	5:	6:	7: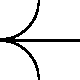

Az ábrákat úgy kell érteni, hogy a villamos szigorúan csak a kirajzolt pályán mozoghat, azaz ha például az 5-ös pályaelemre felülről lép be, akkor csak úgy mehet ki alul, ha előbb kimegy a szomszédos pályaelemre balra,  majd onnan visszajön és lefelé halad tovább. Visszafordulni bármelyik elemről lehet.

Minden pályaelem négyféle állású lehet:

0: az ábrákon látható
1: 90 fokkal az óramutató járása szerint elforgatva
2: 180 fokkal elforgatva
3: 270 fokkal az óramutató járása szerint elforgatva

Feladat:

Készíts programot (VILLAM.PAS, VILLAM.C vagy VILLAM.CPP), amely megadja, hogy egy adott pályaelemről egy másikra a villamos minimum hány lépésben juthat el!

Bemenet:

A VILLAMOS.BE állomány első sorában a térkép sorainak N (1<=N<=100) és oszlopainak M (1<=M<=100) száma van. A következő N sorban soronként M számjegypár - a pályaelemek kódja - található, egy-egy szóközzel elválasztva. Az egyes sorok a térkép egy-egy sorát írják le. A számjegypárok első tagja ta megfelelő ábra száma (0 és 7 közötti érték), a második tagja pedig az elforgatás kódja (0 és 3 közötti érték).
 

00	21	00	00	10
20	70	20	20	30
12	20	00	00	21
70	20	20	30	50

Az utolsó sorban 5 egész szám van: a kezdőelem sor- és oszlopindexe, a belépési irány, valamint a célelem sor- és szolopindexe. A bal felső elem sor- és oszlopindexe (1, 1). A kezdőelem biztosan a pálya szélén van, és feltehetjük, hogy a villamos kívülről érkezett. A belépési irány kódja 0, ha balról lépett be a villamos; 1, ha felülről; 2, ha jobbról és 3, ha alulról.

Kimenet:

A VILLAMOS.KI állomány egyetlen sorába azt a minimális lépésszámot (az egyik elemről a másikra való átlépések számát) kell írni, amely alatt a villamos eljuthat a kezdőelemről a célelemre!

Példa:
 

VILLAMOS.BE	VILLAMOS.KI
4 5 00 21 00 00 10 20 70 20 20 30 12 20 00 00 21 70 20 20 30 50 1 2 1 4 1	12

Megjegyzés:

Egy lehetséges út: (1, 2), (2, 2), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (3, 5), (4, 5), (4, 4), (4, 3), (4, 2), (4, 1)

Elérhető összpontszám: 75 pont + 25 pont a 2. fordulóból