Jill Bates nem szeret hegyet mászni. Jill mindenhova kerékpárral
megy, de mindig a lehető legkönnyebb és legrövidebb utat igyekszik választani.
A jó hír az, hogy Jill Greenhillsben lakik, ahol minden út egy derékszögű
rács mentén épült ki. A Kelet-Nyugat irányú utat utcának, az Észak-Dél
irányú utat sugárútnak nevezzük. Bármely két szomszédos kereszteződés távolsága
egyenlő. A rossz hír az, hogy Greenhillsben sok a hegy, és sok az egyirányú
utca. Jill az útvonal kiválasztásánál az alábbi három szabályt alkalmazza.
1. Elkerüli a 10 méternél nagyobb emelkedést a szomszédos kereszteződések
(rácspontok) között!
2. Soha nem megy forgalommal szemben az egyirányú utcákban!
3. A lehető legrövidebb útvonalat választja!
Írjunk programot, amely segít Jillnek egy elfogadható útvonal megtalálásában!
Bemenet:
Az input állomány a következő formátumban tartalmazza az adatokat:
-
Az első sor két egész számot tartalmaz. Az első egész n; az utcák száma,
a második egész m; a sugárutak száma. (1<=n<=20, 1<=m<=20)
-
A következő n sor a kereszteződések magasságait tartalmazza. Minden sor
egy utcát reprezentál, és pontosan m egészet tartalmaz. Ezek az egészek
az adott utcán lévő kereszteződések méterben mért magasságai.
-
Ezek után egy vagy több sor következik, amelyek az egyirányú utcákat definiálják.
Minden ilyen definíció két pár egész számot tartalmaz, az utca sugárút
utca sugárút formátumban. Az első pár az utca kezdő-, a második
pár az utca végpontját definiálja. Minthogy Greenhills egy szigorú négyzetrács
szerint épült, ezért ha a két pont nem szomszédos, akkor az utca a közbülső
rácspontokon (útkereszteződéseken) is átmegy. Például az
sorozat reprezentálja az 5-7-től 5-8-ig, 5-8-tól 5-9-ig, 5-9-től 5-10-ig
tartó egyirányú utcákat. Az egyirányú utcák felsorolását négy darab 0 zárja
a fenti formátumban.
-
Végül egy vagy több sor következik, amelyek mindegyike két rácspontot tartalmaz
az utca sugárút utca sugárút formátumban. Az első pár Jill
útjának kezdő-, a második végpontjának koordinátái. Az inputot négy darab
0 zárja.
Feltehetjük, hogy az utcák és sugárutak koordinátái a fent definiált határok
között vannak, valamint hogy az utak definíciói szigorúan Észak-Dél, illetve
Kelet-Nyugat irányúak.
Kimenet:
Az input állomány minden kezdőpont-végpont párjára írassuk
ki egy, a szabályoknak megfelelő útvonal rácspontjait! A rácspontot az
'utca-sugárút' formában írjuk ki, az egyes rácspontokat pedig a '->'
karakterekkel kössük össze! Ha Jill szabályainak több útvonal is megfelel,
akkor elegendő egyet kiíratnunk. Ha nincsen a szabályoknak megfelelő útvonal,
vagy a kezdőpont egybeesik a végponttal, akkor egy erre figyelmeztető szöveget
írassunk ki! Minden útvonalleírás után egy üres sornak kell szerepelnie!
Példa:
| INPUT.TXT |
OUTPUT.TXT |
3 4
10 15 20 25
19 30 35 30
10 19 26 20
1 1 1 4
2 1 2 4
3 4 3 3
3 3 1 3
1 4 3 4
2 4 2 1
1 1 2 1
0 0 0 0
1 1 2 2
2 3 2 3
2 2 1 1
0 0 0 0 |
1-1 -> 1-2 1-2 -> 1-3 1-3 -> 1-4 1-4
-> 2-4 2-4 -> 2-3 2-3 -> 2-2
2-3 -> 2-3 : Maradj helyben!
Nincs 2-2 -> 1-1 út. |
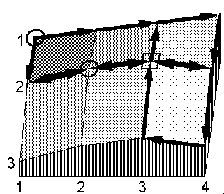
Egy rajzos példa.
Tom azóta lett bélyeggyűjtű, amióta elégedetlen a postások
munkájával. Ha több bélyeg van (értékben) a csomagon, az rossz a postának,
de jó a gyűjtőknek.
A posta igyekszik minimalizálni a szükséges bélyegek számát, amivel
a csomag feladható. A posta munkájának segítened egy, minimumot meghatározó
program megírásával.
A borítékméret korlátozza a ráragasztható bélyegek számát. Például,
ha 1 és 3 centes bélyegek állnak rendelkezésre és 5 bélyegnyi hely van,
akkor 1-től 13 centig tudjuk a borítékot bélyeggel ellátni. Azaz ha 1-13
cent értékű bélyeg kell a csomagra, akkor a feladat megoldható.
| Összeg |
1 centes bélyegek |
3 centes bélyegek
|
|
1
|
1
|
0
|
|
2
|
2
|
0
|
|
3
|
0
|
1
|
|
4
|
1
|
1
|
|
5
|
2
|
1
|
|
6
|
0
|
2
|
|
7
|
1
|
2
|
|
8
|
2
|
2
|
|
9
|
0
|
3
|
|
10
|
1
|
3
|
|
11
|
2
|
3
|
|
12
|
0
|
4
|
|
13
|
1
|
4
|
Öt 3 centes bélyeggel 15 centes értéket is előállíthatunk, de 14 cent
felragasztása nem lehetséges öt darab 1 és 3 centes bélyeggel. A posta
szeretné, meghatározni azt a maximális összeget, ameddig minden érték előállítható
a megadott címletekből összesen adott számút felhasználva. A pédában ez
a maximum 13 cent.
Bemenet:
Minden adatsor első sorában lévő S egész szám a borítékra helyezhető
bélyegek maximális számát adja meg. A második sorban egy N egész, ami az
esetek számát adja meg. Ezután következő N sorban címleteket találunk.
A sorok első száma a címletek száma, majd a címletek következnek növekvő
sorrendben. A címletek legalább 1 szóközzel vannak elválasztva egymástól.
Soronként legfeljebb S névérték szerepelhet! (S<=10, N<=10) A bélyegek
névértéke maximum 100 lehet.
A bemenet a 0 értékkel kezdett adatsorral zárul.
Kimenet:
Az input minden adatsorozatához az output egyetlen sora tartozik,
megadva a folyamatos kitöltéssel elérhető legnagyobb értéket, és az ezt
adó névértéksorozatot a következő formában:
max coverage = <value> : <denominations>
Ha több névértéksorozat adja ugyanazt a folyamatos kitöltéssel elérhető
maximumot, a kevesebb bélyeget igénylő sorozatot kell bejegyezni (ez a
bélyegek nyomtatásakor megtakarítást hoz). Ha a felhasznált bélyegek száma
is egyezik, akkor azt a sorozatot írjuk, ahol a legnagyobb névértékű bélyeg
kisebb. Például, ha 5 bélyeg ragasztható a borítékra, és adott az 1, 4,
12, 21 valamint az 1, 5, 12, 28 sorozat, mindkettővel ki lehet fizetni
71 centig az összes értéket. Mindkettőnél ugyanannyi bélyeget kell felhasználni,
de a legnagyobb címlet az első sorozatban kisebb. Ha több sorozat adja
ugyanazt az értéket ugyanannyi bélyeg felhasználásával, s ráadásul ugyanaz
a névértékmaximum is, bármelyik kiírható.
Példa:
| INPUT.TXT |
OUTPUT.TXT |
5
2
4 1 4 12 21
4 1 5 12 28
10
2
5 1 7 16 31 88
5 1 15 52 67 99
6
2
3 1 5 8
4 1 5 7 8
0 |
max coverage = 71 : 1 4 12 21
max coverage = 409 : 1 7 16 31 88
max coverage = 48 : 1 5 7
8 |
