Nemes Tihamér OKSzTV'95
Második forduló
11-13. osztályosok
1995. január 14. 1100-1500
1. feladat:
(15 pont)
A Kísérleti Fanemesítő Intézet újfajta fenyőfákat nemesített ki. A
fenyőfa törzséből legalább 2 ág ágazik el, vagy egyetlenegy sem. Az egyes
ágak ugyanolyan hosszúak, de feleakkora tömegűek, mint a törzs, s a végükből
újra legalább 2-2 ág ágazik el, vagy egy sem. Ezek megint ugyanolyan hosszúak,
mint amiből kinőttek, de feleakkora tömegűek. Egy fát zárójelekkel és F
betűkkel írunk le a számítógép számára: F (első ág) (második ág) ...
(n. ág) formában. A fának törzse biztosan van.
Példa:
ágnélküli fa: F
kétágú fa: F (F) (F)
sokágú fa: F (F) (F) (F) (F)
bonyolultabb fa: F (F (F) (F)) (F) (F)
Írj programot, amely meghatározza
A. a fa magasságát
(a leghosszabb út hosszát a gyökértől valamelyik ág végéig) - a fenti négy
példában ez 1, 2, 2, illetve 3,
B. a fa tömegét
(feltételezve, hogy a törzs egységnyi tömegű) - a fenti példában ez rendre
1, 2, 3, illetve 2.75,
C. a közös
elágazásból induló ágak számának maximumát - a fenti példában ez rendre
0, 2, 4, illetve 3.
2. feladat:
(16 pont)
Egy városban N(>=1) napon át több televízióadó műsorát lehet fogni.
Egy szöveges állományban tároljuk, hogy melyiken mikor van adás.Egyes adók
bármikor (akár többször is) sugározhatnak műsort, az adásidő egyik napról
a másikra is átnyúlhat, sőt akár N napon át, megállás nélkül is tarthat.
Az állomány minden sorában hét szám található egymástól egy-egy szóközzel
elválasztva, az első az adó sorszáma, a következő három az adás kezdete
(napsorszám, óra, perc), az utolsó három pedig a vége (ugyanilyen jelentéssel)
- az adásidő balról zárt, jobbról nyílt intervallumot jelent. Az órák száma
0 és 24, a percek száma 0 és 59 közötti egész. N értéke az állományban
található napsorszámok alapján határozható meg. Az állomány üres is lehet.
Példa: (egy napon belüli, egész órakor kezdődő és végződő adásokkal)
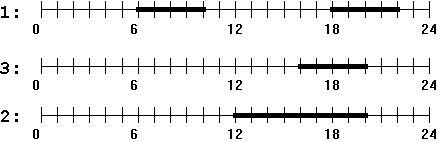
1 1 18 0 1 22 0
1 1 6 0 1 10 0
3 1 16 0 1 20 0
2 1 12 0 1 20 0 |
 |
Írj programot, amely
A.
megadja a leghosszabb olyan időszakot, amikor az állományban tárolt
adatok szerint egyetlen TV-adás sem fogható a városban (a fenti példában:
1. nap, 0.00-6.00),
B.
meghatározza, hogy az N-edik nap melyik percében lehet a legtöbb műsor
közül választani, s akkor hány közül lehet (a fenti példában: 1.nap 18.00
és 19.59 között bármelyik perc jó, ekkor 3 adás fogható).
3. feladat:
(12 pont)
Készíts programot, amely a billetyűzetről tetszőleges sorrendben beolvassa
egy konvex sokszög csúcsainak egész koordinátáit, majd kiírja őket olyan
sorrendben, ahogyan a sokszög oldalai mentén bejárhatjuk őket az óramutató
járásával ellentétes irányban! Kiindulópontnak a sokszög legkisebb x-koordinátájú
csúcsát vedd (ha több ilyen is van, akkor közülük a legkisebb y koordinátájút).
A koordináták biztosan helyesek, nem kell ellenőrizni őket.
A koordinátarendszer a szokásos, a csúcsok koordinátáját az (x,y) egész
számpár adja meg, ahol x az abszcissza és y az ordináta. Az origó a (0,0)
koordinátájú pont, x jobbra, y fölfelé nő.
Példa:
| bemenő számsorozat: |
2 -2 -2 4 -2 -3 1 2 |
| értelmezése: |
(2,-2), (-2,4), (-2,-3), (1,2) |
| az eredmény: |
(-2,-3), (2,-2), (1,2), (-2,4) |
4. feladat:
(12 pont)
Egy kutya úgy úszik át a folyón a túlparton álló gazdájához, hogy minden
pillanatban a gazdi irányába igyekszik. Ezt a mozgást kell közelítő módszerrel
modellezned. A program számítsa ki, hogy a gazdájától milyen távolságra
ér partot a kutya, és ez mennyi ideig tart! Ehhez a következő, valós értékű
paramétereket kell beolvasnia a programnak a billentyűzetről:
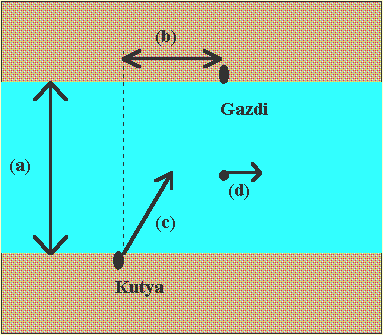 (a) A folyó
szélességét méterben.
(a) A folyó
szélességét méterben.
(b) A gazda távolságát méterben a kutya kezdőpontjának vetületéről
a túlparton (pozitív, ha a folyásiránnyal azonos irányban van, negatív
az ellenkező esetben).
(c) A kutya sebességét (m/s, végig ugyanaz).
(d) A folyó sebességét (m/s, mindenütt ugyanaz).
(e) A közelítés pontosságát, azaz annak az időintervallumnak a hosszát
másodpercekben, amelyen beül a program egyenes vonalú mozgással számolhat.
Grafikus ábrázolás nem szükséges, az értékelésnél nem vesszük figyelembe,
a programod kipróbálást azonban segítheti.
A folyó két partját párhuzamos egyeneseknek tekintjük. A modellezés
akkor álljon le, amikor a kutya már egy méternél közelebb kerül a túlsó
parthoz.
A kutya mozgását haladási iránya, saját sebessége, valamint a folyó
sebessége határozza meg. Mint tudjuk, mindkét sebesség állandó. A haladási
irány, illetve a kutya sebességének a haladási iránytól függő x és y irányú
összetevője azonban csak egy-egy időintervallumon belül tekinthető állandónak.
A kutya haladási irányát az alábbi képlettel számíthatjuk ki:
Irány=ArcTan( (GazdiYKoordináta - KutyaYKoordináta) / (GazdiXKoordináta
- KutyaXKoordináta) ).
(ArcTan: arkusz tangens függvény, megadja, hogy adott tangens érték mekkora
szöghöz tartozik, -pi/2<=ArcTan(x)<=pi/2.)
Egy időintervallum alatt a kutya x irányban
(KutyaSebesség*Cos(Irány)+Vízsebesség)*Időintervallum hossza,
y irányban pedig
KutyaSebesség*Sin(Irány)*Időintervallumhossza
utat tesz meg, hiszen a koordinátarendszert úgy célszerű megválasztani,
hogy a víz az x tengely mentén folyjon.
Példa:
| Bemenet |
Kimenet |
| (a): 200, (b): 100, (c): 5, (d): 6, (e): 1 |
eltelt idő: 157
partot érés távolsága a gazditól kb. 206 |
(a távolság a közelítés miatt valós szám lesz, itt egy közelítő egész
számot adunk meg)
5. feladat:
(20 pont)
Van egy gépünk, amely egy 40 jel hosszúságú
szalagból és egy
író-olvasó fejből áll. Jel egy maximum 40 elemű halmaz, az ábécé
egy-egy eleme lehet. A gép maximum 30 különböző
állapotban lehet.
A gép egy-egy jelet olvas a szalagról (onnan, ahol a fej van). A géphez
tartozó szabálytáblázat írja elő, hogy a beolvasott jeltől és a gép pillanatnyi
állapotától függően mit kell csinálni előbb a szalaggal, amjd a fejjel,
illetve mi lesz a gép következő állapota. Az elvégzendő művelet az ábécé
egy elemének a szalagra írása, a fej jobbra, illetve balra mozgatása vagy
helyben hagyása lehet.
Van a gépnek egy speciális állapota, a végállapot. Ha a gép ebbe az
állapotba kerül, akkor az olvasott jeltől függetlenül leáll. Ha a szabálytáblázatban
nincs a gép aktuális állapotára és az olvasott jelre vonatkozó utasítás,
akkor a gép automatikusan a végállapotba kerül. A gép indulásakor az író-olvasó
fej a szalag 20. pozícióján áll (a sorszámozást az 1. pozíciótól kezdjük)
és az 1-es sorszámú állapotban van.
Írj programot a gép szimulálására!
A GEP.INP állomány első sora a szalagon levő jeleket tartalmazza
(tehát pontosan 40 karakter hosszú). Az állomány további soraiban a szabálytáblázat
elemei vannak, minden sorban egy szabály. A szabályok megadásának sorrendje
tetszőleges. Egy (állapot, jel) párhoz csak egyetlen egy szabály
tartozhat. (Ennek ellenőrzése
nem szükséges.)
A szabályok formátuma: (a1,j1)::(a2,j2,*),
-
ahol a1 az aktuális, a2 pedig az új állapot,
-
j1 az aktuális állapotban olvasott, míg j2 a szalagon a helyébe írandó
jel,
-
a * pedig B, J, vagy - lehet. A B azt jelenti, hogy balra, a J azt, hogy
jobbra kell mozgatni a fejet, míg - esetén nincs mozgatás.
Az állapotokat sorszámukkal jelöljük (a sorszámozás 1-től kezdődik), a
végállapot sorszáma a 0.
A. Ha a gép működése nem fejeződik be 1000
lépésen belül, akkor a
GEP.OUT első sorába a VEGTELEN szót
írjuk.
B. Ha a gép működése közben a fej elhagyja
a szalagot, az első sorba értelemszerűen a HIBA, BALRA KILEPETT
vagy a HIBA, JOBBRA KILEPETT üzenetet írjuk.
C. Ha a gép aktuális állapotára és az olvasott
jelre a szabálytáblázatban nincs utasítás, akkor az első sorba a NEMDEFINIALT
szót,
a második sorba pedig az aktuális állapot sorszámát, egy szóközt és az
olvasott jelet írjuk.
D. Ha a gép működése hibátlanul befejeződik, akkor a file első
sorába a VEGES szót, a következő sorba pedig a szalag tartalmát
írjuk.
Elérhető összpontszám: 75 pont+25 pont az 1. fordulóból
 (a) A folyó
szélességét méterben.
(a) A folyó
szélességét méterben.