Nemes Tihamér OKSzTV'94
Első forduló
9-10. osztályosok
1993. november 23. 1400-1700
1. feladat:
Az óra csak jár (14 pont)
Stopper kezelésére írtunk 3 eljárást. A gettime(or,p,mp,szmp) függvény
a pontos időt adja vissza a paraméterként kapott változókban (óra, perc,
másodperc, századmásodperc). Egy rögzített I paramétert figyelembe véve
a függvények meghívásának sorrendje a következő: Első(I); Második(I); Harmadik(I);
Második(I); Harmadik(I); ... stb.
a) Melyiknek
mi a feladata?
b) Miért használunk
tömböket és mire szolgálnak a K(), E(), V() tömbök?
c) Bizonyos
estekeben a 2. eljárás hibás eredményt számol. Melyek ezek, s hogyan lehetne
kijavítani a programot?
Első(I):
E(I).or:=0; E(I).p:=0; E(I).mp:=0; E(I).szmp:=0
gettime(or,p,mp,szmp)
K(I).or:=or; K(I).p:=p; K(I).mp:=mp; K(I).szmp:=szmp
Eljárás vége. |
Második(I):
gettime(or,p,mp,szmp)
E(I).szmp:=E(I).szmp+szmp-K(I).szmp
E(I).mp:=E(I).mp+mp-K(I).mp
E(I).p:=E(I).p+p-K(I).p
E(I).or:=E(I).or+or-K(I).or
V(I).or:=or; V(I).p:=p; V(I).mp:=mp; V(I).szmp:=szmp
Eljárás vége. |
Harmadik(I):
gettime(or,p,mp,szmp)
K(I).or:=or; K(I).p:=p; K(I).mp:=mp; K(I).szmp:=szmp
Eljárás vége. |
2. feladat:
Táblatalálgatás (13 pont)
Egy táblázatkezelő programról a következőket kell tudni:
-
ún. cellákból áll, amelyek sorokba és oszlopokba vannak rendezve; a sorokat
egész számok (1-től), az oszlopokat betűk (A-tól) azonosítják;
-
Minden cellába egyetlen szám vagy képlet és szám írható (utóbbi esetben
a szám a cella kezdőértéke, a képlet pedig a további valahány kiszámításhoz
alkalmazandó formula);
-
A képletekben bármely cellára hivatkozni lehet az adott cella oszlop- és
sorazonosítójával, pl. C5;
-
A táblázatkezelő a cellák értékét minden lépésben balról jobbra haladva
sor-oszlop sorrendben számolja ki, pl. A1, A2, ..., B1, B2;
-
If(f, A, B) feltételes kifejezés az f feltétel teljesülése esetén az A,
egyébként pedig a B értéket jelenti.
a) Az A1, A2,
A3, A4 cellák kezdőértéke a 0, 1, 1, X. (X tetszőleges pozitív szám.) A
cellák következő értékeit kiszámító képletek:
A1: A1+1
A2: A2+2
A3: A2+A3 |
A képletek alkalmazását addig kell folytatni, amíg A3>A4 nem teljesül.
Mi lesz A1, A2, A3 értéke?
b) Az A1, A2,
A3 cellák kezdőértéke a 0, X, Y. (X, Y tetszőleges pozitív számok.) A cellák
következő értékeit kiszámító képletek:
A1: If(páros(A3),A1,A1+A2)
A2: If(páros(A3),A2*2,A2)
A3: If(páros(A3),A3/2,A3-1) |
A képletek alkalmazását addig kell folytatni, amíg A3=0 nem teljesül. Mi
lesz ekkor A1, A2 értéke?
c) Az A1, A2,
A3 cellák kezdőértéke az 1, X, Y. (X, Y tetszőleges pozitív számok.) A
cellák következő érétkeit kiszámító képletek:
A1: If(páros(A3),A1,A1*A2)
A2: If(páros(A3),A2*A2,A2)
A3: If(páros(A3),A3/2,A3-1) |
A képletek alkalmazását addig kell folytatni, amíg A3=0 nem teljesül. Mi
lesz ekkor A1, A2 értéke?
3. feladat:
Flip-flop (18 pont)
Logikai áramköröket megadhatunk táblázattal vagy logikai formulával.
A feladatban adatábrázolásra használható, tehát állapottal rendelkező áramköröket
specifikálunk.Feltételezzük, hogy az áramkör n+1 időpontbeli állapotát
a bemenő jelek és a kimenő n időpontbeli állapota határozza meg.
|
T=h |
T=i |
| yn=h |
h
|
i
|
| yn=i |
i
|
h
|
Például a T tárolómak van egy bemenete (T) és egy kimenete (y). A táblázat
a kimenet n+1 időpontbeli értékét tartalmazza. Logikai képletekkel ugyanez:
yn+1=(yn és nem T) vagy (nem yn
és T)
a) Adott az
alábbi táblázat. Határozd meg a logikai képletet a lehető legkevesebb művelettel!
Csak az és,
vagy, nem műveleteket használhatod.
|
R=h
S=h
|
R=i
S=h
|
R=h
S=i
|
R=i
S=i
|
| yn=h |
h
|
h
|
i
|
bármi
|
| yn=i |
i
|
h
|
i
|
bármi
|
b) Adott az
alábbi táblázat. Határozd meg a logikai képletet a lehető legkevesebb művelettel!
Csak az és, vagy, nem műveleteket használhatod.
|
J=h
K=h
|
J=i
K=h
|
J=h
K=i
|
J=i
K=i
|
| yn=h |
h
|
i
|
h
|
i
|
| yn=i |
i
|
i
|
h
|
h
|
4. feladat:
Fabejárás (18 pont)
Egy bináris fa rekurzí definíciója a következő:
f=(balrészfa, gyökér, jobbrészfa)
Megengedjük azt is, hogy bármelyik részfa üres legyen (azaz ne tartalmazzon
elemeket). Például egy 3 szintű teljes bináris fa a következő lehet:
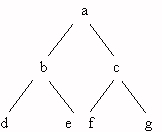 Az
ábrán egy 3 szintű teljes bináris fa látható, a felső szinteken minden
csúcsnak két részfája van, a legalsó szinten egy csúcshoz sem tartozik
részfa (minden részfa üres).
Az
ábrán egy 3 szintű teljes bináris fa látható, a felső szinteken minden
csúcsnak két részfája van, a legalsó szinten egy csúcshoz sem tartozik
részfa (minden részfa üres).
Egy fa összes elemét írja ki a következő rekurzív program az ún. preorder
bejárás szerint:
pre(fa): ha nem üres(fa) akkor írdki(gyökér).
pre(balrészfa), pre(jobbrészfa).
A fenti fára a pre algoritmus a következő eredményt adja: a b d e c f g
Az inorder és a post order bejárás algoritmusa a következő:
in(fa): ha nem üres(fa) akkor in(balrészfa), írdki(gyökér),
in(jobbrészfa)
post(fa): ha nem üres(fa) akkor post(balrészfa),
post(jobbrészfa), írdki(gyökér)
Egy négyszintű teljes bináris fa postorder bejárásával az alábbi betűsorozatot
kaptuk (a fában ugyanaz a betű többször is előfordulhat):
A B C D E F G H G F E D C B A
a) Rajzold fel
a fát!
b) Milyen betűsorozatot
kaptunk ugyanennek a fának az inorder bejárásával?
5. feladat:
Moszat (10 pont)
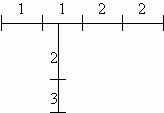 Egy
moszat növekedését formális szabályokkal írjuk le. A moszat minden egységnyi
szakaszának egy számjegyet feleltetünk meg (a szakasz hossza nem függ a
számjegytől!). Ha leágazások keletkeznek, azokat zárójelbe tesszük. Például
az 11(23)22 kódú moszat így néz ki:
Egy
moszat növekedését formális szabályokkal írjuk le. A moszat minden egységnyi
szakaszának egy számjegyet feleltetünk meg (a szakasz hossza nem függ a
számjegytől!). Ha leágazások keletkeznek, azokat zárójelbe tesszük. Például
az 11(23)22 kódú moszat így néz ki:
A moszat növekedését úgy játsszuk le,
hogy kódjában szereplő jeleket
a növekedést leíró szabályok szerinti jelsorozatra cseréljük. Folytasd
4 időegység növekedésének kódjával és ábrájával a megkezdett növekedést!
Szabályok:
| 0->10 |
3->3 |
6->58 |
9->39 |
| 1->32 |
4->56 |
7->3(9) |
(->( |
| 2->3(4) |
5->37 |
8->50 |
)->) |
A növekedés kiindulópontja és első két lépése:
| 4 |
 |
| 56 |
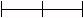 |
| 3758 |
 |
| 33(9)3750 |
? |
| ? |
? |
| ? |
? |
| ? |
? |
6. feladat:
Rajzőrület (12 pont)
Az alábbi program egy térben mozgó teknőcöt vezérlő, LOGO-szerű nyelven
készült.
a) Mit csinál
a belső ciklus a Furcsa(A) eljárásban?
b) Mi a feladata
a külső ciklusnak a Furcsa(A) eljárásban?
c) Mit rajzol
ki az eljárás az A paraméter függvényében?
A programban használt utasítások magyarázata a következő:
| REPEAT db |
a következő, beljebb kezdett
utasításokat db-szor megismétli |
| forward hossz |
előrelép az aktuális irányban
hossz egységgel |
| left szög |
balrafordul szög fokkal a teknőc
síkjában |
| pitch szög |
a teknőc "felfelé" fordul
(függőleges síkban) szög fokkal |
Furcsa(A):
REPEAT 4
forward A
REPEAT 4
pitch 90
forward A
left 90 |
7. feladat:
Egyiket a másik után (18 pont)
Adottak a következő rekurzív függvények:
Nyissz(N,X):
Ha N=1 akkor
X
különben
Nyissz(N-1,elsőutániak(X))
Függvény vége. |
Nyassz(A,B,X):
Ha B=0 akkor
Üres sorozat
különben
Ha A=1 akkor
elejére(első(X),
Nyassz(A,B-1,elsőutániak(X)))
különben
Nyassz(A-1,B-1,elsőutániak(X))
Függvény vége. |
A függvények értelmezése:
első([x1,x2,...,xN])=x1
elsőutániak([x1,x2,...,xN])=[x2,...,xN]
elejére(x0,[x1,x2,...,xN])=[x0,x1,x2,...,xN]
üres sorozat=[]
a) Mit
csinál Nyissz függvény, ha N>0 egész, X sorozat?
b) Mit csinál
a Nyassz függvény, ha A>0 egész, B>=0 egész, X sorozat?
c) Készíts
függvényt egy sorozat N. elemének meghatározására. A függvény leírásában
a fenti sorozatkezelő függvényeket lehet használni.
Elérhető összpontszám: 100 pont
Az
ábrán egy 3 szintű teljes bináris fa látható, a felső szinteken minden
csúcsnak két részfája van, a legalsó szinten egy csúcshoz sem tartozik
részfa (minden részfa üres).