Nemes Tihamér OKSzTV'89

Milyen számot ír ki a képernyőre a következő program?
 

10 I=0 20 GOSUB 50 30 PRINT I 40 STOP 50 GOSUB 60 60 GOSUB 70 70 GOSUB 80 80 GOSUB 90 90 GOSUB 100 100 GOSUB 110 110 I=I+1 120 RETURN

Hol vannak hibák az alábbi BASIC szubrutinban? Javítsd ki!  Milyen állítást fogalmazhatsz meg a változók tartalmáról és a T$ vektor rendezettségéről a megjelölt helyeken (a helyes változatban)? A szubrutin a T$() N elemű vektort rendezné növekvőn.

A DO WHILE ... LOOP ciklus magja mindaddig végrehajtódik, amíg a WHILE mögé írt feltétel teljesül.
 

1000 REM BESZÚRÁSOS RENDEZÉS: 1010 FOR I=2 TO N 1020   IS$=T$ : J=I-1 <--------------------------------------- 1. 1030   DO WHILE J>=1 OR IS$<T$(J) 1040     T$(J)=T$(J+1) : J=J-1 <--------------------------------------- 2. 1050   LOOP 1060   T$(J)=IS$ <--------------------------------------- 3. 1070 NEXT I 1080 RETURN

Mit számít ki az alábbi program, ha az x változó (0<x<1) legfeljebb 2 tizedestört jegyet tartalmaz? Milyen feltételek teljesülése esetén fejeződik be a végrehajtás? Mit ír ki a program x=0.3 esetén?
 

i:=0; w:='0.'; kiír('x:='); beolvas(x); r[0]:=kerekít(x*100); repeat   i:=i+1;   r[i]:=r[i-1]*2;   if r[i]>=100 then begin     r[i]:=r[i]-100;     w:=w+'1';   end   else w:=w+'0';   j:=0;   while ((r[i]<>0) and (r[j]<>r[i]) and (j<i)) do j:=j+1; until not ((i<30) and (j=i)); kiír('Végeredmény: ',w);

Mit csinál az alábbi algoritmus? Az algoritmus egy T$(N,2)-es táblázattal és a K1$, K2$ változókkal dolgozik. Az index függvény egy szöveg karakterei alapján 1 és N közötti egész számot generál. (az 'amíg' ciklus akkor áll le, ha az amíg mögé írt feltétel már nem teljesül.)
 

Eljárás:   K:=index(K1$) : KK:=0   Ha T$(K,1)<>"" akkor     KK:=K     Ciklus       Ha K<N akkor K:=K+1 különben K:=1     amíg KK<>K és T$(K,1)<>""     Ciklus vége   Elágazás vége   Ha KK=K akkor Ki: "baj!!!"   különben T$(K,1):=K1$ : T$(K,2):=K2$ Eljárás vége.

Az alábbi algoritmus egy utcai automata pénzvisszaadásának menetét írja le úgy, hogy a lehet? legkevesebb számú érmét adja vissza. Az FT() vektor írja le, hogy az automata milyen érméket kezel, értéke (20, 10, 5, 2, 1).
 

Pénzvisszaadás (ÖSSZEG):   Cilus I=1-t?l 5-ig     Ha ÖSSZEG>=FT(I) akkor       DB:=INT(ÖSSZEG/FT(I))       KI DB;" db. ";FT(I);" Ft-os"       ÖSSZEG:=ÖSSZEG-DB*FT(I)     Elágazás vége   Ciklus vége Eljárás vége.

Módosítsd a visszaadás algoritmusát, ha azt is tudjuk, hogy az automatának melyik pénzérméből hány darabja van, amit egy D( ) vektorban tárolunk!

Mit rajzol az alábbi, LOGO nyelven írt program, ha tekn?cünk kezdetben a képerny? közepén tartózkodik és felfelé néz? Mi a GVONAL eljárás szerepe? Mit tartalmaz a paramétere?

RIGHT 90 ÁBRA 30

Az ÁBRA és a GVONAL eljárások LOGO definíciója:
 

TO ÁBRA :X   IF :X>9 THEN GVONAL :X LEFT 180 ÁBRA :X*2/3 LEFT 180   GVONAL :X END

TO GVONAL :Y   REPEAT 180 [LEFT 1 FORWARD :Y*3.141592654/180] END

Az utasítások jelentése:
 

RIGHT fok, LEFT fok	jobbra, balra fordulás fok fokkal
FORWARD lépés	elmozdulás előrelépés hosszan
REPEAT db [utasítások]	az utasítások megismétlése db-szor
IF	a THEN ág a sor végéig tart

Az utasításokat egymástól, illetve a paraméterüktől is szóköz választja el. Az eljárások paraméterei elé :-ot kell tenni, az eljárásdefiníció kezdetét TO, végét az END alapszó jelzi.

Egy elektronikus áramköröket gyártó vállalatnak digitális áramkörök hibás kapuit kell megkeresnie. Előzetes tapasztalatok alapján feltételezhető, hogy az ábrán látható áramkörben legfeljebb egy hiba van, és az úgy jelentkezik, hogy valamelyik kapu kimenete a bemeneteitől függetlenül állandóan logikai 0-t ad ki (0-ba ragadt). Ennek megállapításához a G1, G2, G3 kapukból álló áramkör A, B, C bemenetét pedig a 63-as kimenetének 0., 1., 2. bitjére kötöttük, az áramkör Y kimenetét pedig a 64-es bemenet 0. bitjére:

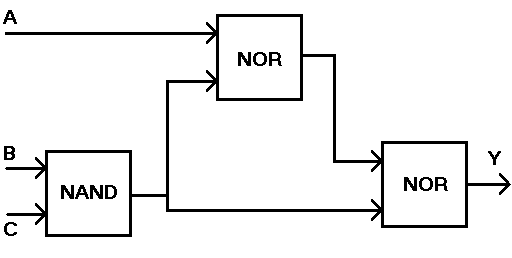
Az egyes kapuk igazságtáblázata (NOR = nem vagy, NAND = nem és):
 

NOR 0 1 0 1 0 1 0 0

NAND 0 1 0 1 1 1 1 0

A következő programmal próbáljuk felfedni a hibákat:
 

10 REM HIBAKERESÉS 20 FOR I=1 TO 3 30   READ X, Y, H$ 40   OUT 63, X     : REM X KIKÜLDÉSE A 63-AS KIMENETRE 50   IF (INP(64) AND 1)<>Y THEN 80 : REM A 64-ES BEMENETEN NEM Y JÖTT 60 NEXT I 70 H$="NINCS 0-BA RAGADT KIMENET" 80 PRINT H$ 90 STOP 100 DATA ?, ?, "G1 HIBÁS" 110 DATA ?, ?, "G2 HIBÁS" 120 DATA ?, ?, "G3 HIBÁS"

Milyen számok kerüljenek a DATA sorokban levő kérdőjelek helyére? Válaszodat indokold meg!

Egy liftet vezérlő program algoritmusát láthatod az alábbiakban. Gondold végig, hogyan működik ez a lift (ezt nem kell leírnod)! Sorolj fel minél több kritikus (kellemetlen) helyzetet, amelybe a lift utasa kerülhet az algoritmus miatt! A HOVA() vektor 32 elemű. (Hívni a liftet valamelyik emeletről lehet, parancsot adni pedig a fülkében.)
 

Liftvezérlő program:   SZINT:=0 : UTASÍTÁSSZÁM:=0   Ciklus     Várj amíg nincs HÍVÁS     Jegyezd föl (HÍVÓGOMB)     Ciklus amíg UTASÍTÁSSZÁM>0       Menj oda(HOVA(UTASÍTÁSSZÁM))       Ajtót nyiss       Várj amíg eltelik 10 másodperc       Ajtót csukj       UTASÍTÁSSZÁM:=UTASÍTÁSSZÁM-1     Ciklus vége   Ciklus vége Program vége.

Menj oda(X):   Ciklus amíg SZINT<>X     Ha SZINT>X akkor Menj le eggyel : SZINT:=SZINT-1     különben Menj föl eggyel : SZINT:=SZINT+1     Elágazás vége     Ha van PARANCS akkor Jegyezd föl(PARANCSGOMB)     Ha van HÍVÁS akkor Jegyezd föl(HÍVÓGOMB)   Ciklus vége Eljárás vége.

Jegyezd föl(GOMB):   Ciklus I=UTASÍTÁSSZÁM-tól 1-ig -1-esével     HOVA(UTASÍTÁSSZÁM+1):=HOVA(UTASÍTÁSSZÁM)   Ciklus vége   UTASÍTÁSSZÁM:=UTASÍTÁSSZÁM+1   HOVA(1):=GOMB Eljárás vége.

(A Várj, amíg ..., a Menj ..., az Ajtót ... tevékenységek végrehajtására, a PARANCS-, illetve HÍVÓGOMB érzékelésére, valamint a PARANCS és HÍVÁS logikai értékek beállítására a lift közvetlenül képes, azokat nem kell definiálnunk.)