Nemes Tihamér OKSzTV 2001

1. feladat: Gráf (20 pont)

Egy irányított gráfot sorszámozott pontokkal és azokat összekötő élekkel adunk meg. A gráfot egy G mátrix írja le, amelyben G(i,j)=1, ha az i-edik pontból vezet él a j-edik pontba, s G(i,j)=0, ha nem. Az alábbi algoritmus egy N pontból álló gráf pontjainak tulajdonságait vizsgálja:
 

Algoritmus:   i:=1; j:=N; k:=1   Ciklus amíg i<>j     Ha G(i,j)=1       akkor j:=j-1       {*}       különben i:=i+1    {**}   Ciklus vége   Ciklus amíg k<=N és (G(i,k)=1 és G(k,i)=0 vagy i=k)     k:=k+1   Ciklus vége   Ha k>N akkor s:=i      {***} Eljárás vége.

A. Milyen tulajdonságú pontok esetén hajtódik végre a {*}-gal jelölt utasítás?
B. Milyen tulajdonságú pontok esetén hajtódik végre a {**}-gal jelölt utasítás?
C. Milyen tulajdonságú pontok esetén hajtódik végre a {***}-gal jelölt utasítás?
D. Lehetséges-e, hogy egy gráfban több olyan tulajdonságú pont is van, mint aminek a sorszámát a {***}-gal jelölt utasításban megadjuk? Magyarázd meg, miért!

Egy kisvárosi bankban N ügyfél szeretne kölcsönt felvenni. Mindegyiknek ismerjük a hitelkeretét, amelyet előbb-utóbb teljesen kihasznál, de egyszerre csak annyit vesz fel, amennyire éppen szüksége van. A bank nem akar annyi pénzt tartalékolni, amennyi a hitelkeretek összege, ugyanis azt feltételezi, hogy az egyes ügyfeleknek nem ugyanakkor van szükségük a hitelre. Ha a bankban van elég pénz, akkor a bankár a hitelkérelmet elfogadhatja, ha nincs, akkor pedig a kérőt várakoztatja. A módszer problémája, ha minden ügyfél éppen újabb hitelt szeretne felvenni (ami még belefér a hitelkeretébe), de a bankban nincs pénz, így mindegyiket várakoztatni kellene. (Ekkor persze visszafizetni sem tudnak, így holtpont-helyzet alakul ki).

A bankár a következő stratégiát találta ki:az igényeket minden hitelkéréskor ellenőrzi, hogy teljesítése esetén kerülhet-e olyan helyzetbe, hogy bárki is kéri a maradék keretét, azt már nem tudja teljesíteni. Ha ilyen helyzetbe kerülne, akkor várakoztatja a hitelkérőt amíg ez a bizonytalan helyzet meg nem szűnik. Ha van valaki, aki több hitelt már nem kérhet, azaz előbb-utóbb visszafizeti a hitelt, akkor ez a helyzet megszűnhet. Ilyenkor a bankár a várakozók igényeit próbálja kielégíteni. Az igényeket az érkezésük sorrendjében igyekszik teljesíteni.

Az alábbi hitelkéréssor, hitelkeret és a bank kezdő tőkéje esetén add meg, hogy a hitelkéréseket és visszaadásokat milyen sorrendben teljesíti a bankár (a sorszámokat ír fel a megfelelő sorrendben)!

A hitelkeretek: Anna - 600, István - 500, Erika - 4000, Ferenc - 700 dollár. A bankban kezdetben összesen 1000 dollár van.

A hitelkérések és a visszafizetések ilyen sorrendben érkeznek:

1. Anna: 100
2. István 100
3. Erika: 200
4. Ferenc 400
5. István: 100
6. Erika: 200
7. Erika: -400 (visszafizet)
8. Anna: 100
9. Ferenc: 300
10. Ferenc: -700
11. Anna: 400
12. István: 300
13. Anna: -600
14. István: -500

Egy lemezegység egyetlen könyvtára N állományt, illetve M blokkot tartalmaz. Minden állomány valahány blokkban helyezkedik el, a blokkokat állományonként láncolva ábrázolják (külön a szabad blokkokat), minden blokknak pontosan 1 láncba kell tartoznia. Az állományszerkezet tartalmazhat láncolási hibákat. Az alábbi algoritmus ezeket próbálja felderíteni.
 
 

Hibafelderítés:   Ciklus i=1-től M-ig     T(i):=0; S(i):=0   Ciklus vége   Ciklus i=1-től N-ig     j:=az i. állomány első blokkja     Ciklus        T(j):=T(j)+1; j:=az i. állomány következő blokkja     amíg j valódi blokksorszám     Ciklus vége   Ciklus vége   j:=első szabad blokk   Ciklus     S(j):=S(j)+1; j:=következő szabad blokk sorszáma   amíg j valódi blokksorszám   Ciklus vége   Ciklus i=1-től M-ig     Ha T(i)>0 és S(i)>0 akkor HIBA1     Ha T(i)=0 és S(i)=0 akkor HIBA2   Ciklus vége Eljárás vége.

A. Milyen hibás esetben hajtódik végre a HIBA1 eljárás?
B. Milyen hibás esetben hajtódik végre a HIBA1 eljárás?
C. Mit kellene beszúrni a legutolsó ciklusba, ha figyelni szeretnénk, hogy egy blokk legfeljebb 1 állományhoz tartozzon?
D. Mit kellene beszúrni a legutolsó ciklusba, ha figyelni szeretnénk, hogy egy blokk csak egyszer szerepeljen a szabad blokkok között?

Egy hegymászó az útja során N pontban feljegyezte, hogy milyen tengerszint feletti magasságban járt. Ezt mutatja az alábbi ábra.

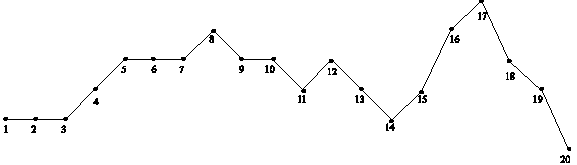
Az i-edik pontban mért tengerszint feletti magasságot Xi-vel jelöljük. Az egyes pon-tok különböző nehézségű szakaszok határán vannak (pl. emelkedő, sík, …). Az alábbi algoritmus ezeket sorolja be 3 csoportba:
 

Pontok:   Ciklus i=2-től N-1-ig     Ha (Xi-Xi-1)*(Xi+1-Xi)>0 akkor Ki: i,’ 1. típusú’ {*}     Ha (Xi-Xi-1)*(Xi+1-Xi)=0 akkor Ki: i,’ 2. típusú’ {**}     Ha (Xi-Xi-1)*(Xi+1-Xi)<0 akkor Ki: i,’ 3. típusú’ {***}   Ciklus vége Eljárás vége.

A.

Az ábrán látható pontok közül milyen sorszámúakat sorol be az algoritmus az 1, 2, illetve 3 típusú pontok közé?

A *-gal jelölt kiírások helyére újabb algoritmusrészleteket teszünk a pontok további osztályozása érdekében:
 

{*}:    Ha (Xi-Xi-1) >0 akkor Ki: i,’ 1/A típusú’                    különben Ki: i,’ 1/B típusú’

{**}:    Elágazás      (Xi-Xi-1)>0 esetén Ki: i,’ 2/A típusú’      (Xi+1-Xi)>0 esetén Ki: i,’ 2/B típusú’      (Xi-1-Xi)>0 esetén Ki: i,’ 2/C típusú’      (Xi-Xi+1)>0 esetén Ki: i,’ 2/D típusú’      egyéb esetben Ki: i,’ 2/E típusú’    Elágazás vége

{***}:     Ha (Xi-Xi-1)>0 akkor       Ha (Xi-Xi-1)+(Xi-Xi+1)>0 akkor Ki: i,’ 3/A típusú’      Ha (Xi-Xi-1)+(Xi-Xi+1)=0 akkor Ki: i,’ 3/B típusú’      Ha (Xi-Xi-1)+(Xi-Xi+1)<0 akkor Ki: i,’ 3/C típusú’    különben      Ha (Xi-Xi-1)+(Xi-Xi+1)>0 akkor Ki: i,’ 3/D típusú’      Ha (Xi-Xi-1)+(Xi-Xi+1)=0 akkor Ki: i,’ 3/E típusú’      Ha (Xi-Xi-1)+(Xi-Xi+1)<0 akkor Ki: i,’ 3/F típusú’    Elágazás vége

B.

Az ábrán látható pontok közül milyen sorszámúakat sorol be az algoritmus az 1/A, 1/B, …, 3/F típusú pontok közé?

A 7 törpe szabadidejében építőkockákból épít tornyokat. Különböző méretű építőkockákkal rendelkeznek, s a toronyépítésnek egyetlen szabálya van: kisebb kockára nagyobbat nem lehet tenni. Az építkezéshez N kockát használnak, az egyes kockát méretét K(i) jelöli (1 <= K(i) <= 99). A kockákat sorban helyezik el, s egy elhelyezett kockát már nem lehet mozgatni. A megoldásban M lesz a tornyok száma, T(j) pedig a j. torony tetején levő kocka mérete.
 
 

Hapci:   M:=1; T(1):=K(1)   Ciklus i=2-től N-ig     j:=1     Ciklus amíg j<=M és K(i)>T(j)       j:=j+1     Ciklus vége     Ha j<=M akkor T(j):=K(i) különben M:=M+1; T(M):=K(i)   Ciklus vége Eljárás vége.

Tudor:   M:=1; T(1):=K(1)   Ciklus i=2-től N-ig     mm:=T(1)     Ciklus j=2-től M-ig       Ha T(j)>mm akkor mm:=T(j)      Ciklus vége     Ha mm<K(i) akkor M:=M+1; T(M):=K(i) különben T(j):=K(i)   Ciklus vége Eljárás vége.

Kuka:   M:=1; T(1):=K(1)   Ciklus i=2-től N-ig     Ha T(1)<K(i) akkor M:=M+1; T(M):=K(i) különben T(1):=K(i)   Ciklus vége Eljárás vége.

A. Milyen elven választják ki a továbbépítendő tornyot az egyes törpék?
B. Állítsd sorrendbe a törpéket aszerint, hogy melyik tudja kevesebb toronyba elhelyezni a kockákat!
C. Milyen kockasorozatra építi mindhárom törpe ugyanazt az egy tornyot (N>2)?
D. Adj olyan kockasorozatot (N=5), amelyre a törpék mind különböző számú tornyokat építenek!

Elérhető összpontszám: 100 pont