Nemes Tihamér OKSzTV 2000

1. feladat: Karesz a robot (18 pont)

Karesz, a robot egy egyszerű világban él, amelyet egy négyzetráccsal lehet leírni. A zsebében köveket hordhat, amelyeket letehet a négyzetrács mezőire, illetve felveheti az ott talált követ. Kezdetben a terület közepén (az ábrán K-val jelölt helyen) áll, északi irányba néz és nincs nála kő. (A köveket fekete pöttyök jelzik.)

Eljárás:   Ismételd amíg nem érsz ki     Ha van nálad kő, akkor Tegyél le egyet     Lépj előre     Ha van ott kő akkor       Vegyél fel egyet       Fordulj balra       Lépj előre     Elágazás vége   Ismétlés vége Eljárás vége.

Példa:

 

* **       K

Karesz a 3. lépése után ér ki. (a 4.-re már lelépne) A kilépésig a szürke mezőkön jár. A köveket a jelzett helyen hagyja.

*   **

Az alábbi kezdőállapotok esetén add meg, hogy
 
1. hány lépés (a Lépj előre utasítás végrehajtásai száma) után lép le Karesz a négyzetrácsról.
2. mely mezőkön jár a kilépésig
3. hol maradnak kövek?
 

* *   * *                         K

*     *   *                       K                     *   *     *

*   * **       *   *     *         K                     *     *   *

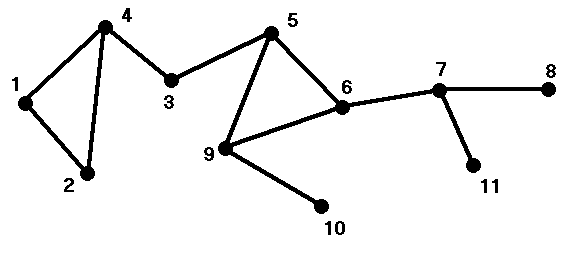
Egy irányítatlan gráfot a G(N,N) csúcsmátrixszal ábrázolunk, azaz G(I,J) pontosan akkor IGAZ értékű, ha a gráfban az I. és a J. csúcsot él köti össze. Két tetszőleges csúcs között legfeljebb egy él lehet, önmagával egyetlen csúcsot sem köt össze él. Az alábbi algoritmus bizonyos éleket töröl a gárfból. Az S vektor elemeinek értéke kezdetben 0.






Törlés:   Ciklus I=1-től N-ig     Ciklus J=I+1-től N-ig       Ha G(I,J) akkor S(I):=S(I)+1 : S(J):=S(J)+1     Ciklus vége   Ciklus vége                                             (*)   Ciklus     I:=1     Ciklus amíg I<=N és S(I)<>1       I:=I+1     Ciklus vége     Ha I<=N akkor                          (**)       S(I):=0       J:=1       Ciklus amíg nem G(I,J)         J:=J+1       Ciklus vége       S(J):=S(J)-1 : G(I,J):=hamis : G(J,I):=hamis     Elágazás vége   amíg I<=N   Ciklus vége Eljárás vége.

A. Mit tartalmaz az S vektor a (*)-gal jelölt helyen? Add meg a konkrét példa esetén is!
B. Milyen csúcsok esetén jutunk el a (**)-gal jelölt részre? Add meg a konkrét példa esetén is!
C. Milyen élek maradnak végül a gráfban? Add meg a konkrét példa esetén is!
 

Az alábbi algoritmusok az A vektort használják bemenetként. A vektor elemeit az angol ábécé kisbetűivel indexeljük, értékük nemnegatív szám.
 

Kiszámol(A,N):   N:=0     Ha A(J)>0 akkor N:=N+A(J)   Ciklus vége Eljárás vége.

Mitcsinál(I,N,A,B):   Ha I=N+1 akkor Ki(B,N)            (*)   különben     Ciklus J='a'-tól 'z'-ig       Ha A(J)>0 akkor         B(I):=J : A(J):=A(J)-1         Mitcsinál(I+1,N,A,B): A(J):=A(J)+1       Elágazás vége     Ciklus vége   Elágazás vége Eljárás vége.

Előbb a Kiszámol(A,N), utána a Mitcsinál(1,N,A,B) eljárást hajtjuk végre. A Ki(B,N) a B vektor elemeit írja ki 1-től N-ig. Az alábbi kérdésekre szöveges választ adj!

A. Mit ír ki a (*)-gal jelölt sorban, amikor a kiírást először végrehajtjuk (hogyan függ a kiírás az A vektor tartalmától)?
B.Hányszor hajtja végre a (*)-gal jelölt sorban lévő kiírást?
C. A (*)-gal jelölt sorban a kiírások eredményei milyen sorrendben követik egymást?

A prioritási sor olyan adatszerkezet, amelybe új elemeket a fontosságuknak megfelelő helyre lehet beilleszteni (a kisebb értékűek előbbre kerülnek, mint a nagyobbak), a sort elhagyni azonban csak a sor elején álló tudja. A prioritási sort jelképezi a következő ábra.

Egy K (1<K<=N) hosszúságú prioritási sort használunk az N elemű A vektor rendzésére az alábbi módon:
 

Rendezés:   Ciklus I=1-től K-ig     Sorba(A(I))   Ciklus vége   Ciklus I=K+1-től N-ig     Sorból(B(I-K)): Sorba(A(I))   Ciklus vége   Ciklus I=1-től K-ig     Sorból(B(N-K+I))   Ciklus vége Eljárás vége.

Legyen kezdetben N=8, K=4 és az A vektor a következő: 5, 4, 3, 6, 8,, 5, 9, 7.

A. Írd le cikluslépésenként a prioritási sor tartalmát (mindhárom ciklusra)!
B. Mi a feltétele általában annak, hogy az eredmény valóban rendezett legyen?
C1. Hányszor kell végrehajtani ezt az algoritmust egy tetszőleges kiinduló sorozaton, hogy biztosan rendezett legyen az eredmény?
C2. Milyen bemenetre kell valóban ennyiszer végrehajtani?

Rekurzív ábrák (ún. fraktálok) generálását egy rekurzív formulával (szövegesen) adhatjuk meg. A formula egyik tagja (az ún. axióma) megadja az alapábrát,.a másik pedig a helyettesítési szabályokat, amit az első tagra kell alkalmazni, az előírt darabszámszor.

A formulákban rajzoláskor az F betű 1 egységnyi rajzolást jelent az aktuális irányban, az X betű hatására semmit nem kell csinálni, a + balra fordulást, a - jobbra fordulást jelent (ennek szögét az axiómákban adjuk meg).



Példa:

Axióma: F szög(+,-): 90 fok
Helyettesítési szabály: F=F+F-F
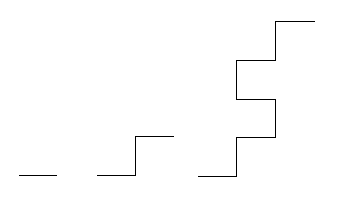
Az első helyettesítés után az axiómából keletkezik: F+F-F
A második helyettesítés után az előzőből keletkezik: F+F-F+F+F-F-F+F-F
A kezdőábrák, valamint a helyettesítéssel kapott ábrák az alábbiak.


Az alábbi két formulapárhoz
A. rajzold le az alapábrát!
B. add meg, hogy a kiinduló ábrát leíró szöveg hogyan változik, ha a helyettesítési szabályokat egyszer, illetve kétszer alkalmazzuk.
C. Valamint rajzold le az így keletkező, a generálásnak megfelelő ábrákat!
 

	1.	2.
axióma	F--F--F	FXF
szög (+,-)	60 fok	120 fok
helyettesítlési szabályok	F=F+F--F+F	F=FXF X=+FXF-FXF-FXF+

Elérhető összpontszám: 100 pont