Nemes Tihamér OKSzTV 2000

1. feladat: Karesz a robot (21 pont)

Karesz, a robot egy egyszerű négyzetrácsos világban él. A zsebében köveket hordhat, amelyeket séta közben a négyzetrács mezőiről szedhet fel. Egy-egy követ az ábrákon egy-egy fekete pötty jelöl. Kezdetben a terület közepén, az ábrán K-val jelölt helyen áll, északi irányba néz és nincs nála kő.
 

Eljárás:   Ismételd amíg nem érsz ki     Ha van ott kő akkor        Vegyél fel egyet       Fordulj balra     Különben Lépj előre     Elágazás vége   Ismétlés vége Eljárás vége.

Példa:

 

** *       K

Karesz a 4. lépése után ér ki. (az 5.-re már lelépne) A kilépéskor 2 kő van a zsebében. Kilépésig a szürke mezőkön jár.

*

Az alábbi kezdőállapotok esetén add meg, hogy
 
1. hány lépés (a Lépj előre utasítás végrehajtásai száma) után lép le Karesz a négyzetrácsról.
2. kilépéskor hány kő van a zsebében,
3. mely mezőkön jár a kilépésig?
 

* *   * *                         K

*     *   *                      **** K                     *   *     *

*   **                       *   K              ***         *

Egy kiszámolós játékban N gyerek körbe áll az ábrának megfelelően.



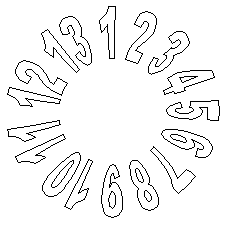
Az alábbi három algoritmus különféle kiszámolási szabály szerint működik. Kezdetben az A logikai vektor összes eleme (1-től N-ig) igaz értékű.

A. Add meg, milyen sorrendben írja ki a három algoritmus a kiszámolt gyerekek sorszámát, ha kezdetben N=13 és K=5?
B. Melyek kerülhetnek végtelen ciklusba, s mi ennek a feltétele?
 

Első:   I:=K : A(I):=hamis : Ki(I) : J:=1   Ciklus amíg J<N     I:=I+K : Ha I>N akkor I:=I-N     Ha A(I) akkor A(I):=hamis : Ki(I) : J:=J+1   Ciklus vége Eljárás vége.

Második:   I:=K : A(I):=hamis : Ki(I) : J:=1   Ciklus amíg J<N     L:=0     Ciklus amíg L<K       I:=(I mod N)+1       Ha A(I) akkor L:=L+1     Ciklus vége     A(I):=hamis : Ki(I) : J:=J+1   Ciklus vége Eljárás vége.

Harmadik:   I:=K : A(I):=hamis : Ki(I) : J:=1 : Ha K>1 akkor K:=K-1   Ciklus amíg J<N     L:=0     Ciklus amíg L<K       I:=I-1 : Ha I=0 akkor I:=N       Ha A(I) akkor L:=L+1     Ciklus vége     A(I):=hamis : Ki(I) : J:=J+1 : Ha K>1 akkor K:=K-1   Ciklus vége Eljárás vége.

Egy rajzgépet a RAJZ S utasítással lehet vezérelni, ahol S szöveg típusú változó. A szövegben grafikus utasítások szerepelhetnek (E, K, D, N - észak, kelet, dél, nyugat). A megfelelő betű hatására a rajzgép tolla 1 egységgel elmozdul (és így rajzol) az adott irányba.

Példa:

 

RAJZ "EEKKDDNN" a négyzetrács bal alsó sarkából indulva az alábbi képpontokat festi be:

A. Mit rajzol a RAJZ "EEEKKDKKKKEKKDDDNNNDNNENNN" utasítás hatására?
B. Miben más a RAJZ f(S) utasítás hatására készülő rajz. mint a RAJZ S, ha az f függvény az alábbi?
 

B1.	f(S):   Ciklus I=1-től hossz(S)-ig     Ha S(I)="E" akkor T(I):="D"     különben Ha S(I)="D" akkor T(I):="E"              különben T(I):=S(I)   Ciklus vége   f:=T Függvény vége.
B2.	f(S):   Ciklus I=1-től hossz(S)-ig     Ha S(I)="E" akkor T(I):="K"     különben Ha S(I)="K" akkor T(I):="D"              különben Ha S(I)="D" akkor T(I):="N"              különben T(I):="E"   Ciklus vége   f:=T Függvény vége.

Egy rendezőpályaudvaron K sínpárra tudják tolni a vagonokat. Egy hosszú szerelvény érkezik, amelyben N-féle helyre menő vagon van. Egy sínpárra egyszerre csak ugyanarra a helyre menő vagonokat tolhatunk, s onnan visszatolni már nem szabad. Ha egy sínpáron olyan helyre küldendő vagonok állnak, amelyek az érkező szerelvény további részében már nincsenek, akkor azokat el kell indítani a célállomás felé, s a sínpár másik szerelvény összeállításához használható. Az egyes vagonokat a célállomás neve azonosítja.

Példa:

Ha 3 sínpár van és az érkező szerelvény az a, b, a, b, c, a, c helyre küldendő vagonokból áll, akkor 2 sínpárral megoldható a feladat. Az elsőre toljuk az a célállomásra menőket, a másodikra előbb a b-re menőket, s amikor a 4. kocsival végeztünk, a szerelvényt a második vágányról elindíthatjuk, s a helyére most már a c állomásra menők kerülhetnek.
Így a két vágányra kerülő vagonok sorszámai: 1: 1, 3, 6, illetve 2: 2, 4, 5, 7

A. Mi a feltétele, hogy minden célállomásra egyetlen szerelvényt kell küldeni?
B. Hány sínpárt kell minimálisan használni, ha minden célállomásra egyetlen szerelvényt kell küldeni?
C. Add meg a minimálisan használandó sínpárok számát, valamint, hogy az egyes sínpárokra az eredeti szerelvény milyen sorszámú kocsijait kell tolni az alábbi két példára (a megoldáshoz legfeljebb 3 sínpárt használhatsz):
C1. a, a, b, a, c, a, d, a, b, d, b, d
C2. a, a, b, a, c, a, d, c, d ,e, e, d

Egy rekurzív programozási nyelvben egy mondat szavaira az alábbi függvényeket alkalmazhatjuk.
 

szószám(Mondat)	a mondat szavai számát adja
első(Mondat)	a mondat első szavát adja
utolsó(Mondat)	a mondat utolsó szavát adja
elsőutániak(Mondat)	a mondat összes szavát adja a másodiktól az utolsóig
utolsóelőttiek(Mondat)	a mondat összes szavát adja az utolsót elhagyva
elejére(Szó, Mondat)	a szót a mondat elejére illeszti, s ez lesz az eredmény
végére(Szó, Mondat)	a szót a mondat végére illeszti, s ez lesz az eredmény

Add meg, hogy az alábbi rekurzív függvények milyen sorrendben írják ki az "EGY KETTŐ HÁROM NÉGY ÖT HAT HÉT NYOLC KILENC TÍZ" mondat szavait!
 

A(M):   Ha szószám(M)>0 akkor végére(első(M),A(elsőutániak(M)))   különben M Függvény vége.

B(M):   Ha szószám(M)>2 akkor     elejére(első(M), elejére(utolsó(M),                              B(elsőutániak(utolsóelőttiek(M)))))   különben M Függvény vége.

C(M):   Ha szószám(M)>1 akkor     elejére(első(M),C(elsőutániak(elsőutániak(M))))   különben M Függvény vége.

D(M):   Ha szószám(M)>1 akkor     végére(első(M),elejére(első(M),D(elsőutániak(M))))   különben M Függvény vége.

Elérhető összpontszám: 100 pont